中学数学の食塩水に「食塩」を混ぜる問題（その2）

2018年7月3日2023年1月15日食塩水の濃度実用数学技能検定（数学検定数検),数検3級

読了時間: 約5分21秒

[mathjax]

Lukia

前回始まった「食塩水に『塩』を混ぜ合わせる」問題ですが、
さっそく今回で終了です。
とはいえ、今回は、不等式が含まれていますので、少し難しいかもしれません。
がんばってみてくださいね。
それでは、以下に問題を示します。
スクロールの手を止めて、解いてみてください。

問題

濃度10%の食塩水が340gある。
これに食塩を加えて、濃度を15%以上、20%以下になるようにしたい。
加える食塩の重さの範囲を求めよ。

Lukia

なお、今回はふたつの式を立てなくてはならないので、
まずは、「15％以上」のほうの式を立て、
そのあとで、「20％以下」のほうの式を立てていきます。

15％以上

表に書き込む。

もも

15％以上、20％以下って、ちょっと難しそうですね。
ま、でもまずは表を描いてみます。

もも

横長の線を3本と、それを4等分するように縦の線を3本引きます。

Lukia

ももちゃんは、以下のような表を描いています。

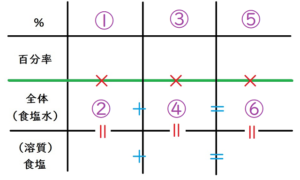
もも

問題文によると、
①は10、
②が340ですね。

もも

「食塩を加えて」とあるから、
③は100でよさそう。

もも

問題文の一番下に「加える食塩の量」とあるから、
④は $\Large x$ としてよさそうですね。

Lukia

確認しておくと、ももちゃんがおいた③の100は、
食塩には、食塩が100％含まれている。ということからきています。

もも

⑤は15で・・・
⑥は、「横はたし算」ルールによって、
②+④=⑥とわかるから、
$\Large \left( 340+x\right)$ とおけます。

％を百分率に直しておく。

もも

百分率に直すのは簡単。
左から、$\Large \frac{10}{100}$ ・ $\Large \frac{100}{100}$ ・ $\Large \frac{15}{100}$ です。

縦はかけ算・横はたし算

Lukia

では、「縦はかけ算」をして、一番下の段のマスをうめていきましょう。

もも

はい。
まず、食塩水の列は、
$\Large \frac{10}{100}\times 340$ となります。

もも

次に、食塩の列は、
$\Large \frac{100}{100}\times x$ となります。

もも

できあがる食塩水の列は、
$\Large \frac{15}{100}\times \left( 340+x\right)$ となります。

一番下の段の「たし算」をする。

Lukia

手慣れたもんですね。
それでは、いよいよ「横はたし算」をして、式を立ててみましょう。

もも

はい。
式は、
$\Large \frac{10}{100}\times 340+\frac{100}{100}\times x=\frac{15}{100}\times \left( 340+x\right)$ となります。

Lukia

はい。方程式だったらまったく問題ない式なのですが、
今回は、15％以上ということなので、「不等式」にしなければなりませんね。

もも

あっ、そうですね。
このままだったら、濃度15％の食塩水ができてしまいますね。

不等式を考えてみる。

Lukia

ちなみに、表の一番下の段は、「食塩の重さ」となっていますね。
ここを見ながら考えてみましょう。

Lukia

濃度10%の食塩水には、いま、34ｇの食塩が含まれています。
これは、もう、どうがんばっても増えません。
できあがる食塩水を濃く（全体に対して、食塩の重さが多く）なるためには、
加える食塩の重さでしか、調整できないんですね。

もも

はい。

Lukia

ということは、
左辺の「10%食塩水に食塩を加えたときの食塩の重さ」が、
右辺の「15%食塩水に含まれる食塩の重さ」と同じか、それよりも重くなってほしい。
と言いたいのですが、数学の記号でそれを表せるもの、知りませんか？

もも

$\Large \geq$ とか、$\Large \leq$ かな？
ほかにも、$\Large \gt$ とか、$\Large \lt$ もありますね。

Lukia

そうですね。
今回は、15%以上とありますから、きっかり15%も含まれています。
ゆえに、$\Large \geq$ か、$\Large \leq$ を使いましょう。
ちなみに、広がっている方が、左辺と右辺のどっちに向けばいいですか。

もも

10％食塩水と食塩を混ぜたほうに重くなってほしいんだから・・・
左辺ですね。

Lukia

そうです。ですから、あらためて式を立てると、
$\Large \frac{10}{100}\times 340+\frac{100}{100}\times x\geq\frac{15}{100}\times \left( 340+x\right)$ となりますね。
計算自体は、方程式のときと同じようにできますよ。

もも

ということは、
まず分母の100をはらって、
$\Large 10\times 340+100\times x\geq 15\times \left( 340+x\right)$ になり、

もも

左辺を $\Large x$ 、
右辺を340でまとめて、
$\Large \left( 100-15\right)x\geq \left( 15-10\right)\times 340$ にします。

もも

両辺を5でわって、
$\Large 17x\geq 340$ とします。
計算して、
$\Large x\geq 20$ が導かれますね。

Lukia

または、両辺を2倍してから計算する方法もあります。
$\Large 2\left( 100-15\right)x\geq 2\left( 15-10\right)\times 340$ とし、
$\Large 170x \geq 10\times 340$ の両辺を170で割ります。
そして、
$\Large x \geq 20$ を導きます。
このへんの計算のくふうは、その人の好みですね。

Lukia

さて、答えが $\Large x \geq 20$ となりましたから、
加える食塩は、20ｇ以上ということになりますね。

20％以下

Lukia

こちらも操作は同じなので、式は、ふきだしなしで書いていきますね。

$$\Large \frac{10}{100}\times 340+\frac{100}{100}\times x \leq \frac{20}{100}\times \left( 340+x\right)$$
両辺の分母の100をはらって、
$$\Large 10\times 340+100\times x \leq 20\times \left( 340+x\right)$$

Lukia

左辺を $\Large x$ 、右辺を340でまとめて、

$$\Large \left( 100-20\right)x \leq \left( 20-10\right)\times 340$$
$$\Large 80x \leq 3400$$
$$\Large x \leq 42.5$$
ゆえに求める食塩の量の範囲は、
$$\Large 20 \leq x \leq 42.5$$

Lukia

つまり、
20ｇ以上、42.5ｇ以下　となります。