2019年冬の火曜ドラマ「初恋(はじこい)」に出ていた数学の問題を解いてみる。

[mathjax]
一粒で二度おいしいドラマ?
深田恭子さん主演のTBSの火曜ドラマ『初めて恋をした日に読む話』略して初恋、おもしろいですよね〜。
ヒロイン春見順子は、東大を不合格になってから、母との関係がギクシャクし、塾講師業も契約切れギリギリの状態に。
何もかもうまくいかない順子ですが、ふとしたきっかけで、髪の毛がピンク色の高校生、由利匡平を東大に合格させるべく奮闘し始めます。
奮闘を通して彼女がかつての輝きを取り戻し始めると、なぜか空前のモテ期到来。
順子をめぐる恋愛模様、はたまたユリユリは東大理Ⅲに合格できるのか?

Lukia
そんな大見栄切っちゃって大丈夫なの?ユリユリ・・・。
2019年2月現在、私大の試験や、国公立の二次試験をひかえた、まさに受験生の人は、ドラマどころじゃないと思いますが、
この春から「まさに受験生」になるいわば、「プレ受験生」の人たちは、勉強のヒントも得られたりするので、さまざまな楽しみ方ができるのではないかと思います。
ドラマ自体がおもしろかったので、原作の漫画も読みたくなりましたが、
全8巻ですか・・・。
|
|
まずは、ドラマを楽しみたいと思います。(^◇^;)
眠れる龍、春見順子。
ドラマを見ていて驚いたのが、春見順子のポテンシャルの高さです。
順子と出会ったときの由利の学力は、高校2年生ながら中学内容もおぼつかないありさまでした。
それでいて、「オレを東大に合格させてくんね?」なんて言うわけですから、
その後しゃかりきになった順子でも、最初は戸惑ったと思います。
順子が由利に対して まずさせたことは、入塾テストをもとにした中学内容の総ざらい。
驚いたのは、順子が中学内容をすべて一人で教え切って、ユリユリを「中学卒業」させたことです。
教える側にとって、中学内容は、高校内容とは別の難しさがあります。
高校内容では、中学内容をもとに さらっと説明して流してしまう部分がいろいろとあるのですが、
ユリユリは、その基礎部分が出来上がっていないので、順子は「基礎工事」を完遂させなければなりません。
そして、その「基礎工事」は、教える側も十二分な中学内容の知識がインプットされていることが前提となります。
たしかに「知識がある」からといって、誰でも上手に「教えられる」わけではありません。

Lukia
しかし、「教える」ならまずは、当人が十二分な「知識」をインプットしている必要があるわけです。
そうしてみると、私は、順子が、塾講師としては何年もくすぶっていたものの、彼女の学力そのものがまったく衰えていないことに驚きました。
(塾で、中学生も担当していたのかな。)
中学校以降になると、教える側も専門の教科・科目に分かれますが、順子は、中学理科だろうと英語だろうと数学だろうとなんでも教えてしまうのです。

Lukia
また、由利が「中学卒業」レベルに到達し、晴れて高校内容を教えていっても、
順子はポテンシャルの高さを維持しています。
どうやら、高校内容も全教科できそうな雰囲気なのです。
ドラマでは、毎話、英語・古文・社会(倫理)・数学などといろいろな授業のシーンが出てきます。
教え方そのものは、あんまりうまくない。
けれど、東大に落ちたとはいえ、彼女のポテンシャルが非常に高いことだけはよくわかります。
なんだって彼女のポテンシャルは、眠っていたんでしょう。
彼女が眠れる龍であることに気づき、叩き起こす上司や同僚はいなかったのでしょうか。
ユリユリのように、彼女をその気にさせる生徒はいなかったんでしょうか。

Lukia
ドラマ『初恋』には「講義」監修の人がいるのかも。
ちなみに、ドラマでは有能な先生。とか、有名大学に何人も合格させたスーパー講師。という設定であっても、たいていの板書は死んでいます。
授業シーンのほんの一瞬を切り取るのですから、板書そのもののクオリティは問われません。
ですから、単に書いただけの「雰囲気」板書が多いです。
しかし、なまじっか経験者だと、そういうところが気になります。

Lukia

Lukia

Lukia
どんな流れにしたら、こんな素っ気ない板書になるんかね。
こんな調子で、ドラマを見ているんだか、毒づいているんだかわからなくなるので、
自然と、教育に携わる人が出てくるドラマは見なくなりました。
そんなわけで、『初恋』も初回お試しのつもりで見てみたのですが、
思ったよりも工夫がこらされているので、なんだかんだで見続けています。
とはいえ、初めのころの英語の仮定法を教えているシーンはひどかった。
順子は、地頭はいいけど、教える能力はまだまだのヘタレ塾講師でした。

Lukia
と思っていましたし、

Lukia
と内心毒づいておりましたが、
古文を教えているシーンでは、マグネットプレートを多用するなんて工夫をし、格段に授業力が高まっていました。
順子の「教える」能力も少しずつ向上している。という設定なのかもしれませんね。
これ、「線形計画法」っていうんだ!
第4話で、順子のいとこ八雲が、
「それ、線形計画法使うと楽だぞ。」と順子の生徒に言うシーンがあります。
順子は、八雲に「それ、数学Ⅱ(範囲)で、まだ(その子は前の段階にいるので)教えてないから、言わないで!」と言います。
順子が生徒の進捗状況をしっかり把握しているということを示しているんでしょうね。
そして、いよいよユリユリに「線形計画法」を教える段階がやってくるわけですが、
ドラマを一時停止して、その問題をじっくり見てみました。

Lukia
何て名前か知らなくても、問題は解けるってことですね。(笑)
順子の体に隠れて一部問題が見えなかったのですが、おそらくこういう問題であろうと思いますので、問題を示し、実際に解いてみようと思います。
問題
\( \ x+y \ \)がとり得る最大値を求めよ。
\( \ x \geq 0\quad \quad \quad \cdots\cdots\quad ① \ \)
\( \ y \geq 0\quad \quad \quad \cdots\cdots\quad ② \ \)
\( \ x+2y \leq 10\quad \cdots\cdots\quad ③ \ \)
\( \ 3x+2y \leq 18\quad \cdots\cdots\quad ④ \ \)
まずは、動ける範囲を明らかにする。

Lukia
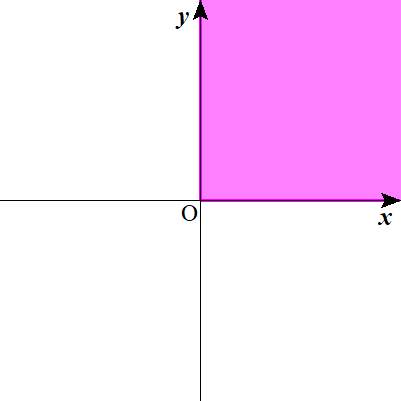
また、この動ける範囲のことを特に「領域」といいますが、
\( \ y \ \)軸そのものの\( \ y \geq 0 \ \)の部分や、
\( \ x \ \)軸そのものの\( \ x \geq 0 \ \)の部分も領域に含まれています。

Lukia
$$\begin{align}x+2y \leq &10 \\\\ 2y \leq &-x+10 \\\\ y \leq &-\frac{1}{2}x+5 \end{align}$$
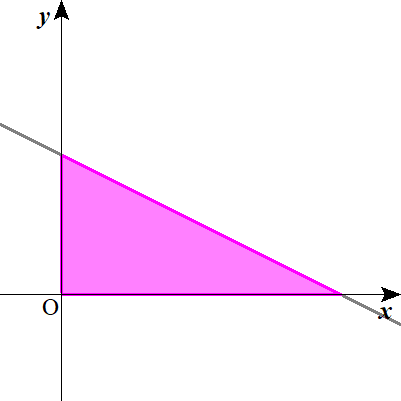
つまり、\( \ y \ \)の座標は、直線\( \ y=-\frac{1}{2}x+5 \ \)上か、その下側に存在する。ということになります。

Lukia
不等式③が加わることによって、上の図のような直角三角形の三辺上とその内部に座標\( \ \left( x \ , \ y\right) \ \)が存在できることになりました。

Lukia
$$\begin{align}3x+2y \leq &18 \\\\ 2y \leq &-3x+18 \\\\ y \leq &-\frac{3}{2}x+9 \end{align}$$
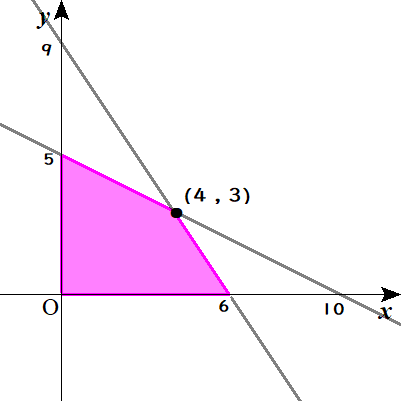
不等式③のときと同じように、\( \ y \ \)の座標は、直線\( \ y=-\frac{3}{2}x+9 \ \)上か、その下側に存在する。ということになります。

Lukia
通常は、不等式③や不等式④を方程式(直線の式)とみなし、グラフに直線を書き込んでいきます。
すると、交点があるとわかりますので、連立方程式を解いて、交点の座標を求めておくわけですね。
ちなみに、交点の座標は、\( \ \left( 4 \ , \ 3\right) \ \)とわかります。
定数kの最大値を求めていく。
4つの不等式より、領域は以下の図のとおり。(境界を含む。)

$$\begin{align}x+y=&k\quad \left( ただし\quad k \ は実数\right) \quad とおく.\ 求める最大値は,直線 \ y=&-x+k\quad の切片である\ &kの最大値と一致する. \end{align}$$

Lukia
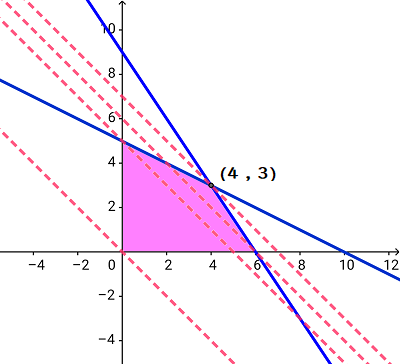
傾き\( \ -1 \ \)の直線を想定し、(ものさしで作ってみてください)それをピンクの領域からはみださないように傾きを維持したまま動かします。
そのとき、\( \ y \ \)軸に最も高い位置で交わるのはどこか?と聞かれていることになるのです。

Lukia
4つの点線がそれぞれ\( \ y \ \)軸(縦の矢印)と交わっている位置(高さ)を見比べてみてください。
すると、座標\( \ \left( 4 \ , \ 3\right) \ \)を通るときの\( \ y \ \)切片の値が最も大きいことがわかりますね。
グラフより,
$$\begin{align}k \ は,&直線 \ y=-x+k\quad が\left( 4 \ , \ 3\right)を通るとき最大値をとる. \ k=&4+3=7 \ 求める最大値は\quad &7 \end{align}$$

Lukia
今後もドラマ中でおもしろいなと思うことがあれば、つたないながらも解説してみたいと思います。
ユリユリ、2019年2月現在の受験生、どっちもがんばれ~~~!
[subscribe2]












ディスカッション
コメント一覧
まだ、コメントがありません