高校数学の絶対値の問題は、グラフでイメージしよう。（その3）

2018年9月7日2023年1月15日数と式実用数学技能検定（数学検定 数検),数検準2級

[mathjax]

問題

$$\begin{align}&xについての二次方程式\\\\ &\vert x^2-2x-3 \vert=k \left( k は実数\right)\\\\ &が成り立つとき、解の個数を求めよ。 \end{align}$$

Lukia

一見むずかしそうですが、グラフが描ければ解ける問題です。

グラフを描こう。

$$\begin{align}y=&\vert x^2-2x-3 \vert として考える。\\\\ =&\vert \left( x+1\right)\left( x-3\right) \vert \\\\ =& \pm \left( x+1\right)\left( x-3\right)\\\\ & \\\\ y=& \left( x+1\right)\left( x-3\right)　　ただし、x \leq -1 , 3 \leq x　　のとき\\\\ y=&- \left( x+1\right)\left( x-3\right) 　　ただし、-1 \leq x \leq 3　のとき \end{align}$$
グラフは、以下のようになります。

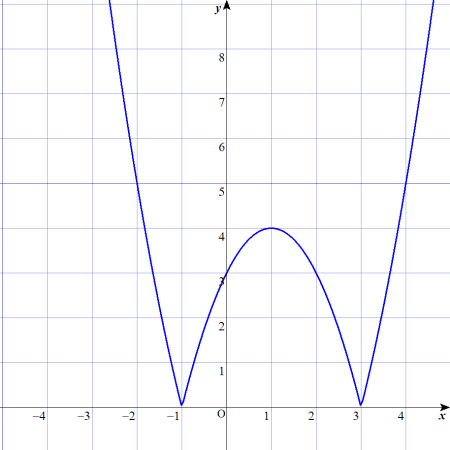
Lukia

上部分にちょっと描き足したら、歯みたいですね。（笑）

kはいくつだよ！

$$\begin{align}&これまでの右辺は、8とか2など、ある意味、具体的な数字でした。 \\\\ & \\\\ &しかし、今回の右辺は、\color{red}{実数k}となっています。\\\\ & \\\\ &これは、\color{red}{kは実数であれば、なんでもいいよ～。}という意味なんですね。\\\\ & \\\\ &y=k　,すなわち、x軸に平行でありさえすれば、どんな値でもオッケ～なんです。\\\\ & \ & \\\\ &このように、なんでもオッケーと言われたら、\\\\ &こちらから、kの範囲を定めて、答えていく必要があります。\\\\ & \\\\ &さて、今回求めるのは、「解の個数」でした。\\\\ &つまり、y=\vert x^2-2x-3 \vert と、y=kの交点の個数の変化をとらえましょう。\\\\ & という問題なんですね。\\\\ & \\\\ &というわけで、「交点の個数の変化」をとらえていきます。 \end{align}$$

緑の線と青の線の交点を数えてみよう。

$$\begin{align}&今回、\color{green}{y=k}は、\color{green}{緑の線}で示すことにしました。\\\\ &\color{green}{kは実数}であればよいので、\color{green}{正でも負でも0でもよい}ことになります。\\\\ &　\\\\ &また、青の線と緑の線の交点を\color{red}{赤い点}で示しています。\end{align}$$

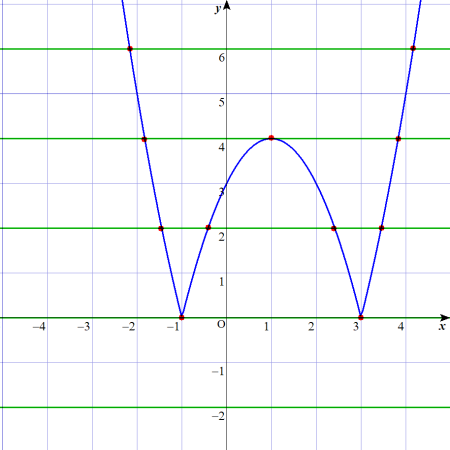
$$\begin{align}ⅰ）y=&6 のとき。\\\\ &赤い点は2つあります。\\\\ &ちなみに、緑の線をx軸に平行なまま、上下にスライドしてみてください。\\\\ &上にスライドさせても、ずっと交点は2個のままです。\\\\ &下は、y=4のとき、交点が3つになるので、4.00000001とか、\\\\ &限りなく4に近い数字までは交点は2のままですね。\\\\ &ここから、4 \lt k のとき、交点すなわち解は2個ということになります。\end{align}$$
$$\begin{align}ⅱ）y=&4　のとき。 \\\\ &赤い点は3つあります。\\\\ &ゆえに、k=4 のとき、解は3個ということになります。 \end{align}$$
$$\begin{align}ⅲ）y=&2　のとき。 \\\\ &赤い点は4つありますね。\\\\ &ここで、緑の線をx軸に平行なまま、上下にスライドさせてみてください。\\\\ &k=4に近づくまでは、ギリギリ4個の交点を保ち、\\\\ &k=0になるまでは、ギリギリ4個を保っています。\\\\ &ゆえに、0 \lt k \lt 4 のとき、解は4個ということになります。 \end{align}$$
$$\begin{align}ⅳ）y=&0　のとき。 \\\\ &赤い点は2個ありますね。\\\\ &ゆえに、k=0 のとき、解は2個ということになります。 \end{align}$$
$$\begin{align}ⅴ）y=&-2 のとき。\\\\ &青い線が存在しないので、交点もありませんね。 \\\\ &ゆえに、k \lt 0 のとき、解なしとなります。\end{align}$$

こたえ

$$\begin{align}ⅰ）からⅴ）をまとめると、\\\\ 0 \lt k \lt 4　のとき、&解4個 \\\\ k=4　のとき、&解3個\\\\ k=0 ,または 4 \lt k　のとき、&解2個\\\\ k \lt 0 のとき、&解なし\end{align}$$

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。