高校数学の絶対値(その2）の練習問題

2018年9月6日2023年1月15日数と式実用数学技能検定（数学検定 数検),数検準2級

[mathjax]

次の式のグラフを描け。

$$\begin{align}①& y=\vert 2x-3 \vert \\\\ \\\\ ②& y=2\vert x \vert \\\\\ \\\\ ③& y=\vert x^2+x-6 \vert \end{align}$$

①

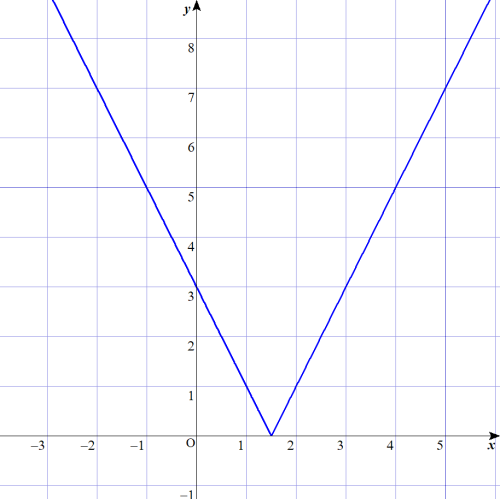
$$\begin{align}y&=\vert 2x-3 \vert \\\\ y&= \pm \left( 2x-3\right) \\\\ & \\\\ y&=2x-3　 \left(ただし \frac{3}{2} \leq x　のとき\right) \\\\ y&=-2x+3　 \left(ただし x \leq \frac{3}{2}　のとき\right) \end{align}$$

②

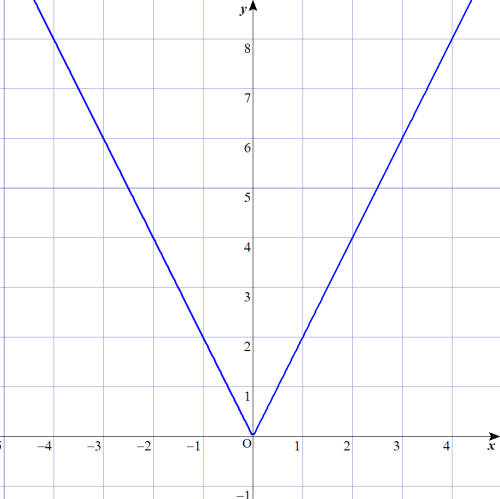
$$\begin{align}y&=2\vert x \vert \\\\ y&= \pm 2x \\\\ & \\\\ y&=2x　　\left( ただし 0 \leq x　のとき\right) \\\\ y&=-2x　　\left( ただし　x \leq 0　のとき\right) \end{align}$$

③

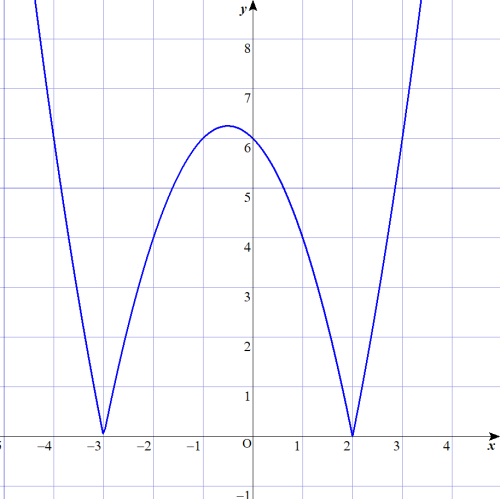
$$\begin{align}y&=\vert x^2+x-6 \vert \\\\ y&=\vert \left( x+3\right)\left( x-2\right) \vert \\\\ y&= \pm \left( x+3\right)\left( x-2\right)\\\\ & \\\\ y&=x^2+x-6　　\left(ただし、-3 \leq x , 2 \leq x　のとき\right)\\\\ y&=-x^2-x+6　　\left(ただし -3 \leq x \leq 2　のとき\right) \end{align}$$

次の方程式を解け。

$$\begin{align}①& \vert 2x-3 \vert=7 \\\\ \\\\ ②& 2\vert x \vert=4\\\\ \\\\ ③& \vert x^2+x-6 \vert=0 \end{align}$$

①

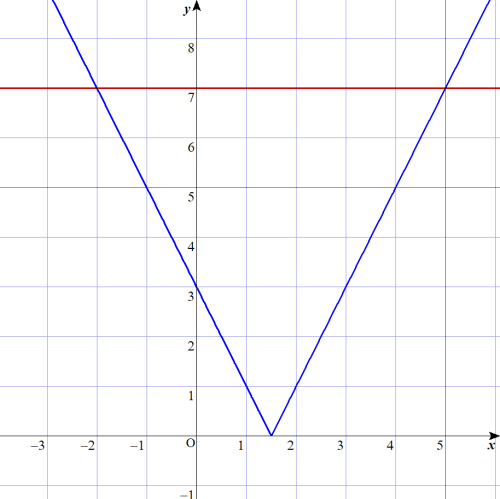
$$\begin{align}&\color{blue}{\vert 2x-3 \vert}=\color{red}{7} \\\\ &\color{blue}{ \pm \left( 2x-3\right)}=\color{red}{7} \\\\&ⅰ）　 \color{blue}{2x-3}=\color{red}{7}　 \left( \frac{3}{2} \leq x\right) 　を解いて、x=5 \\\\&ⅱ） \color{blue}{-2x+3}=\color{red}{7}　　 \left( x \leq \frac{3}{2}\right)　を解いて、x=-2 \\\\ &以上より、x=5 , -2 \end{align}$$

②

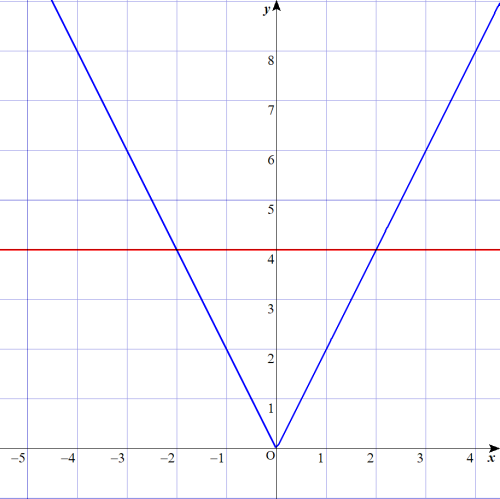
$$\begin{align}\color{blue}{2\vert x \vert}=&\color{red}{4} \\\\ \color{blue}{\vert x \vert}=&\color{red}{2} \\\\ \color{blue}{ \pm \left( x\right)} =&\color{red}{2} \\\\ ⅰ）　\color{blue}{x}=&\color{red}{2}　　 \left( 0 \leq x\right) \\\\ⅱ） \color{blue}{-x}=&\color{red}{2}　　\left( x \leq 0\right) \\\\ 以上より、x=&2 , -2 \end{align}$$

③

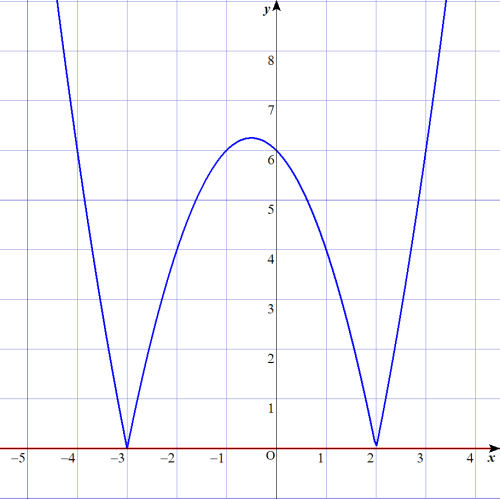
$$\begin{align}\color{blue}{\vert x^2+x-6 \vert}=&\color{red}{0} \\\\ \color{blue}{\vert \left( x+3\right)\left( x-2\right) \vert}=&\color{red}{0} \\\\ \color{blue}{ \pm \left( x+3\right)\left( x-2\right)}=&\color{red}{0} \\\\ & \\\\ ⅰ）　\color{blue}{\left( x+3\right)\left( x-2\right)}=&\color{red}{0}　　\left( x \leq -3 , 2 \leq x\right) のとき、x=-3 , 2\\\\ ⅱ）\color{blue}{-\left( x+3\right)\left( x-2\right)}=&\color{red}{0}　　\left( -3 \leq x \leq 2\right) のとき、x=-3 , 2\\\\ 以上より、x=&-3 , 2 \end{align}$$

[subscribe2]