高校数学の絶対値の問題は、グラフでイメージしよう。（その2）
[mathjax]
問題
$$\Large \vert x+3 \vert=8 を満たすx を求めよ。$$
「ひと手間」かける式変形で解く。
高校で教わるのはこのパターンのようですね。
$$\begin{align}\vert x+3 \vert&=8 \\\\ \pm \left( x+3\right)&=8 \\\\ x+3&= \pm 8\\\\ x&=-3 \pm 8\\\\ &x=5,-11 \end{align}$$
数学は、視覚化できるとわかりやすい。
たしかに、この程度の問題であれば、グラフを描くよりも正確に式変形をして解いていくほうが速いです。
しかし、できれば、式を視覚化（グラフ化・イメージ化）できたほうが、より数学は解きやすく、楽しくなります。
というわけで、グラフを描きながら考えていきたいと思います。
$$y=\vert x+3 \vert を描いてみる。$$
$$\begin{align}&xy平面上で考えるため、\\\\ &\vert x+3 \vert=8 を\\\\ &y=\vert x+3 \vert と、y=8 に分けます。\\\\ &y=\vert x+3 \vert を考えてみましょう。\end{align}$$
$$もしも、y=x+3 であったら、下図のようになりますね。$$
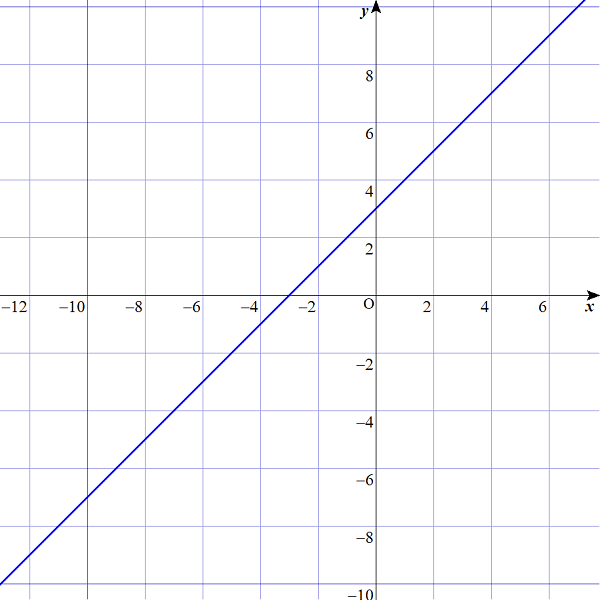
$$\begin{align}&しかし、y=\vert x+3 \vert の場合は、このグラフを描けばバツとなってしまいます。\\\\ &絶対値を「x軸との距離」と考えることにしたのですから、\\\\ &yの値がマイナスになってはマズイのです。 \end{align}$$
$$\begin{align}&しかし、このグラフのx \leq -3 の範囲を見ていくと、\\\\ &yの値、すなわち向きこそマイナスとなっていますが、\\\\ & x軸との距離はちゃんと存在していますね。\\\\ &「距離（量・大きさ）」は正の値で示されるので、\\\\ &たとえば、x=-6のとき、たとえば、x=-8のとき・・・などと\\\\ & 距離の値をグラフに描きこむと、\\\\ & x \leq -3の青い実線が、青い点線に移り変わったことがわかります。\\\\ & \\\\ &つまり、絶対値を含んだグラフを簡単に描きたいなら、\\\\ &x軸で折り返せばよいことになりますね。\end{align}$$
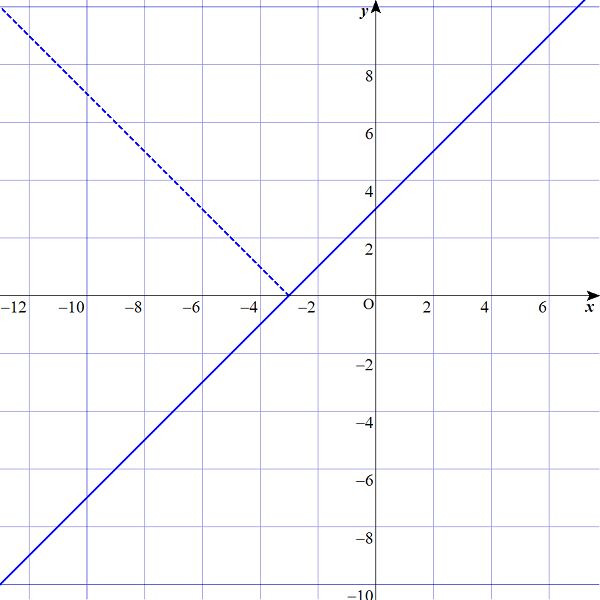
あらためて解いてみる。
式変形をしていくと、次のようになります。
$$\begin{align}y&=\vert x+3 \vert \\\\ y&= \pm \left( x+3\right)\\\\ &\\\\ y&=x+3 \left( -3 \leq x\right) \\\\ y&=-x-3 \left( x \leq -3\right) \end{align}$$
また、グラフは以下のように示されます。
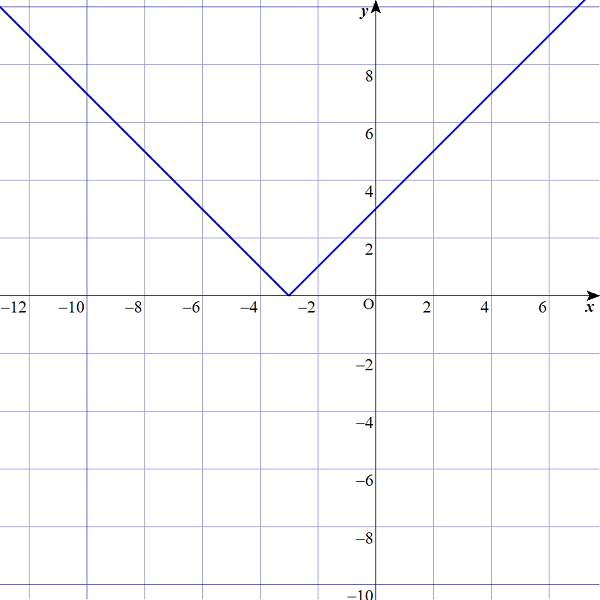
$$\begin{align}&式変形だけですと、範囲の設定が難しいと思うのですが、\\\\ &グラフを描けば、x=-3で、グラフが変わることがすぐにわかりますね。 \end{align}$$
問題を視覚でとらえる。
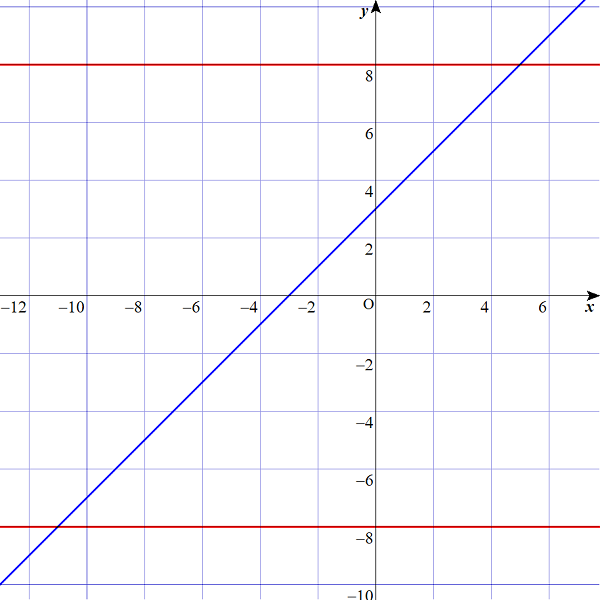
$$\begin{align}y&=\vert x+3 \vert のグラフが描けたので、\\\\ y&=8 を描き加えて、答えを求めてみましょう。\\\\ y&=8 は、赤い線で示します。 \end{align}$$
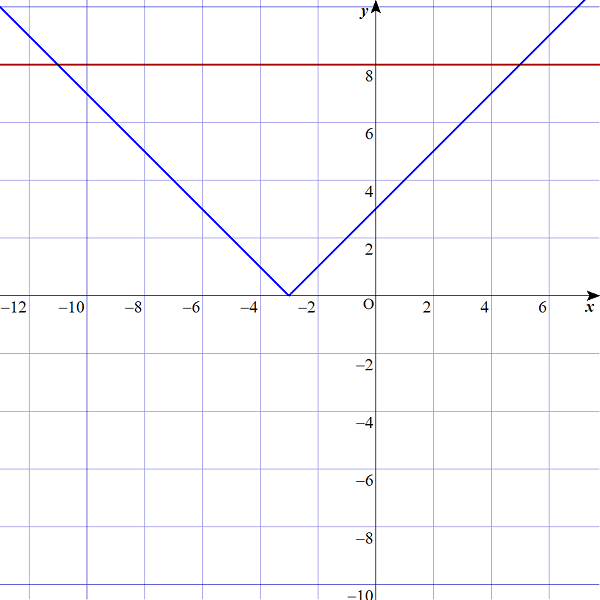
$$\begin{align}&\color{blue}{青の線}と\color{red}{赤の線}が交わったところが\\\\ &求めるxの値となります。\\\\ &ゆえに、x=-11 , x=5 となります。 \end{align}$$
「式変形」だけでは、限界が来る。
ちなみに、この記事の冒頭にある「式変形」パターンをグラフ化すると、次のようになります。
式中の青い文字、赤い文字は、下のグラフの線の色と対応させています。
$$\begin{align}\vert x+3 \vert&=8 \\\\ \pm \left( x+3\right)&=8 \\\\ \color{blue}{x+3}&= \color{red}{\pm 8}\\\\ x&=-3 \pm 8\\\\ &x=5,-11 \end{align}$$
$$\begin{align}たしかに&、このレベルなら、式変形で十分解けます。\\\\ しかし、&\vert x+3 \vert+\vert 2x-4 \vert=8 のように、絶対値記号が二つ出てきたり、\\\\ 右辺も絶&対値だったりしたら、頭が混乱してしまいかねません。\\\\ 範囲をイ&メージ化できる力がなければ、行き詰まってしまうことになります。\\\\ なるべく&たくさんの問題を解いて、ぱっとイメージ化できるようになってください。 \end{align}$$
練習問題
$$\begin{align}次&の式のグラフを描け。 \\\\ ①& y=\vert 2x-3 \vert \\\\ ②& y=2\vert x \vert \\\\ ③& y=\vert x^2+x-6 \vert \end{align}$$
$$\begin{align}次&の方程式を解け。\\\\ ①& \vert 2x-3 \vert=7 \\\\ ②& 2\vert x \vert=4\\\\ ③& \vert x^2+x-6 \vert=0 \end{align}$$
共有:
プロフィール
