高校数学の絶対値の問題は、グラフでイメージしよう。(その10)

[mathjax]
自宅のパソコンでブログ記事を書いていたはずが、
突然不思議な世界に迷い込み、
高校生?恐竜、ディノさんと出会ってしまった私。
ディノさんは、絶対値の問題の解き方を教えてくれたら、ひらけた場所までの案内をしてくれると言いますが・・・
さて、今日の問題の「解法」で、ディノさんは私を「解放」してくれるのでしょうか。
![]()
問題
$$\Large \vert \vert x-1 \vert -2 \vert-3=0$$
左辺をなるべくシンプルにしたい。

Lukia
「左辺をなるべくシンプルに。」です。
手っ取り早く、シンプルにできるところはありませんか?

ディノ
これは、すぐにはどうにかできないな。
・・・まてよ、左辺にある\(-3\)って、当分の間関係ないよな。
ということは、\(-3\)を右辺に移項しておけば、絶対値に集中できるぞ。

Lukia

ディノ
というわけで、
\(\Large \vert \vert x-1 \vert -2\vert=3\)
として、考えることにする。
絶対値記号を内側からはずす。

ディノ
う~ん、図を描きたいけど、難しい!
絶対値が二つあるけど、絶対値の中に絶対値があるんだから、これまでのV字がふたつのパターンは使えなさそうだ。

Lukia
でも、もう一度思い出してほしいのですが、
もしも、\(\vert \vert x-1 \vert-2 \vert\)が
\(\left( \left( x-1\right)-2\right)\)だったら、
ディノさん、どうしてましたか?

ディノ
その後、外側のかっこもはずすよな。
・・・あっ!そういうことか!!

Lukia
今回の絶対値も、内側の絶対値から考えればよいんです。

ディノ
簡単な図を描いてみよう。

ディノ
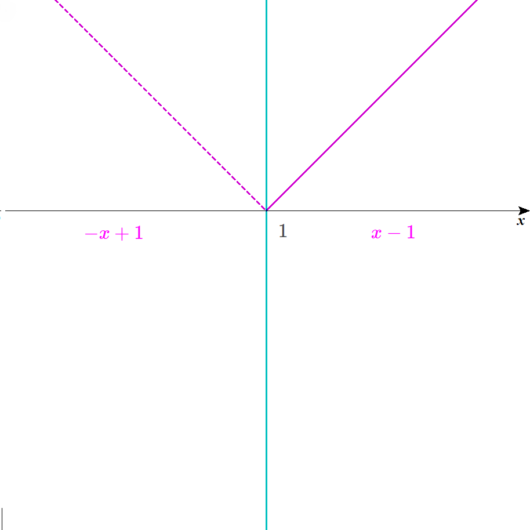

ディノ
\(\color{magenta}{1 \leq x}\)のとき、\(\color{magenta}{y=x-1}\)となり、
\(\color{magenta}{x \leq 1}\)のとき、\(\color{magenta}{y=-x+1}\)となる。
式を書き直してみる。

Lukia
外側の絶対値に視野を広げて、式を書きなおしてみてください。

ディノ
\(\color{magenta}{1 \leq x}\)のとき、
\(\Large y=\vert \color{magenta}{x-1}-2 \vert\) となる。
・・・整理して、
\(\Large \color{magenta}{1 \leq x}のとき、y=\vert x-3 \vert\)だ。

ディノ
\(x \leq 1\)のとき、
\(\Large y=\vert \color{magenta}{-x+1}-2 \vert\) となるな。
・・・整理して、
\(\Large \color{magenta}{x \leq 1}のとき、y=\vert -x-1 \vert\) だ。
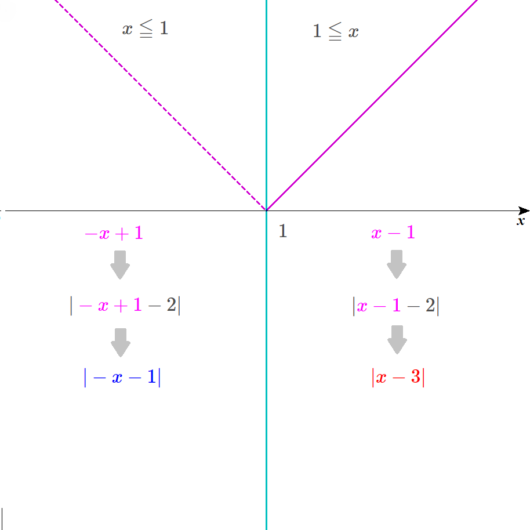

Lukia
縦にもう2本の線が加わって、4つの範囲に分けられそうですね。
範囲を細かく設定しよう。

ディノ

Lukia
単純に考えるとそうなりますね。
まずは、右の範囲から片付ける。

ディノ
\(1 \leq x\)のとき、
\(y=\color{red}{\vert x-3 \vert}\)だ。

ディノ
\( 3 \leq x\)のとき、
\(y=\color{red}{x-3}\)で、
\(x \leq 3\)のとき、
\(y=\color{red}{-x+3}\)となる。

Lukia

ディノ
・・・いや、伸びない!
\(x \leq 1\)の範囲は、左の式の縄張りだからな。

Lukia
ということは、右から二番目の範囲は、もう少し細かく設定してやる必要がありますね。

ディノ
\(1 \leq x \leq 3\)のとき、
\(y=\color{red}{-x+3}\)となるな。
次に左の範囲を片付ける。

ディノ
じゃ、次は、いよいよ左の範囲だ。
まず、\(x \leq 1\)のとき、
\(y=\color{blue}{\vert -x-1 \vert}\) だ。

ディノ
\(y=\color{blue}{x+1}\)となり、
\(x \leq -1\) のとき、
\(y=\color{blue}{-x-1}\)となる。

ディノ
\(-1 \leq x \leq 1\) に限定されるんだよな。
範囲ごとに式を書き込んでいく。

ディノ
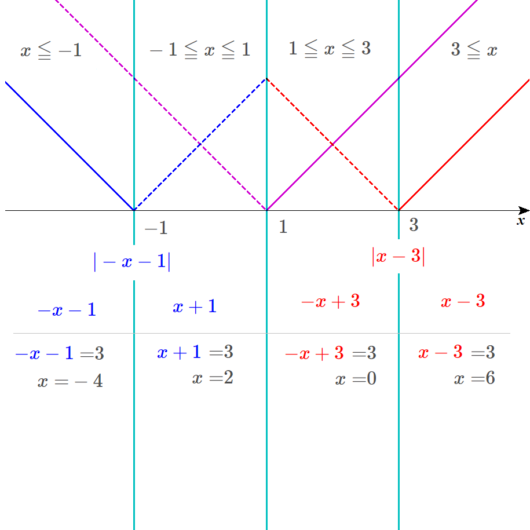

Lukia
お見事です!
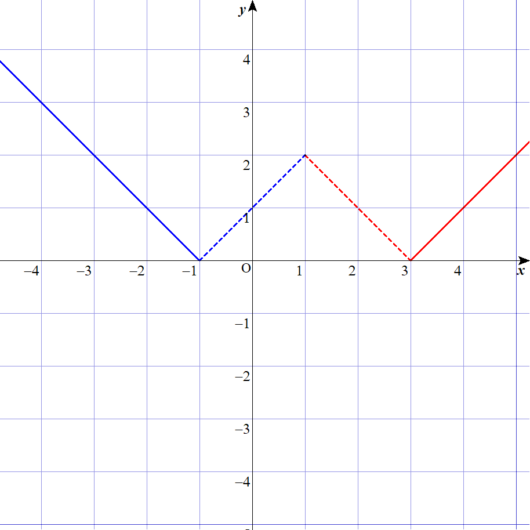
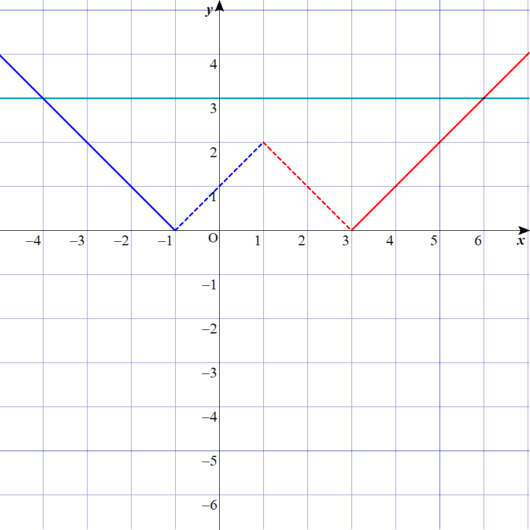
グラフを描くとこうなる。

ディノ
こうなるよな。
方程式を解く。

ディノ
あとは、\(=3\)をつけて、方程式を解けばいいんだな。

Lukia

ディノ
まず、左端の範囲は、
\(\color{blue}{-x-1}=3\)より、
\(x=-4\)だ。

ディノ
\(\color{blue}{x+1}=3\)より、
\(x=2\)だ。

ディノ
\(\color{red}{-x+3}=3\)より、
\(x=0\)だ。

ディノ
\(\color{red}{x-3}=3\)より、
\(x=6\)だ。

範囲を比較して答えを出す。

Lukia
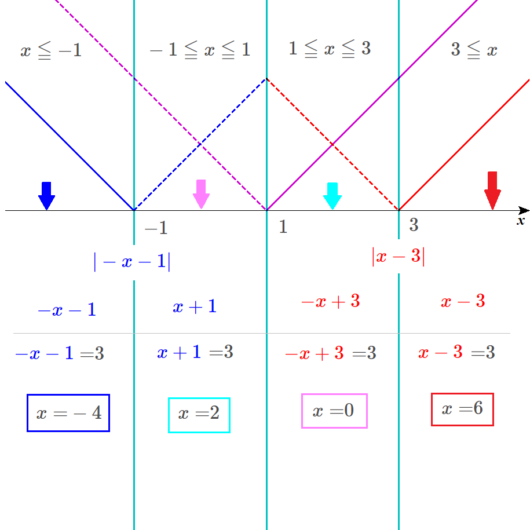
左端の範囲の解は、青い四角で囲み、\(x\)軸には、青い矢印で、だいたいの位置を示します。
左から二番目の範囲の解は、水色の四角で囲み、\(x\)軸には、水色の矢印で、だいたいの位置を示します。
右から二番目の範囲の解は、桃色の四角で囲み、\(x\)軸には、桃色の矢印で、だいたいの位置を示します。
右端の範囲の解は、赤い四角で囲み、\(x\)軸には、赤い矢印で、だいたいの位置を示します。

ディノ
ということは、この二つの解は、不適だ。
こたえ
$$\Large \vert \vert x-1 \vert-2 \vert-3=0$$
$$\Large x=-4 , x=6$$
![]()
さよなら、ディノさん。(のはずが?)

ディノ
たしかに、2点でしか交わってないな。

Lukia
でも、ちょっとずつ分解していけば、なんとかなる。というのがわかってもらえたんじゃないかと思います。

ディノ

Lukia
(あれっ!ディノさん、ピンと来てない!?)
恐竜とはいえ、今どきの子だったようです。(うう、世代間ギャップ・・・)

Lukia
この問題は、仕上げというか、力試し的な問題としてとりあげました。
ディノさんは、私がちょっとのヒントを出した以外は、ほとんど自力で解いていましたから、絶対値に関しては自信を持っていいと思いますよ。

ディノ

Lukia
さて。絶対値の問題もクリアできましたし、私が元の世界に帰れる方法を教えてもらえますよね?

ディノ
今日が最後になるだろうなと思って、ここへ連れてきたんだ。

Lukia
お知らせしていませんでしたが、ここはディノさんがしげく通っているドーナツ屋さんです。

ディノ
で、「絶対値がわかんねぇよ〜〜〜」って思って、ドーナツ食ったら、店の奥にある掃除道具入れのドアから、
すげ〜光がもれてさ。
で、ドア開けたら、なぜか森みたいなんが続いてて、歩いてたらお前がいたわけよ。

Lukia
な、なるほど・・・。
じゃ、今回も同じようにすれば・・・
いや、でも、もう絶対値はわかったわけだから、「わかんねぇよ〜〜〜」は使えないでしょ?

ディノ

Lukia
さっすが、暴君。(ティラノサウルスを日本語訳すると、暴君トカゲとなります)
読者の皆様、私自身にストーリー展開の才能はないので、このレベルでお許しください。

ディノ

Lukia
でも、出会えてよかったです。楽しかったですし。
これからも、数学がんばってくださいね。

ディノ
お互い名残惜しかったけれど、ディノさんが、「絶対値がわかった〜〜〜!」という強い喜びの感情を持ちながらドーナツにかぶりつくと、
たしかにお店の奥にある掃除道具の扉から強い光がもれはじめました。
おそるおそる開けてみると、そこには私がやってきたような森が広がっていました。
急いで森に足を踏み出し、奥へ奥へと進むうち・・・
私は、自分の部屋のパソコンの前に座っていました。

Lukia
いや、夢だったのかもな。
考えてみれば、恐竜が、スイーツ好きな男子高校生で、数学やってるなんて、へんてこりんな設定です。
恐竜好きな私が、夢の中であれこれとごちゃまぜにしてしまったんだろうと思っていました。
しかし、どうやらこのブログ内で、ディノさんは確実に存在するようになってしまったのです。
それは、Yahoo!知恵袋から絶対値がらみの問題を見つけて解いていたときのこと。

ディノ

Lukia

ディノ
いや〜、なんでもできちゃって、自分で自分が恐いぜッ。

Lukia
恐竜が、スイーツ好きな男子高校生で、数学やってるという無茶な設定の上、
むりくりパラレルワールドに行って帰ってきたのに、
その上、そんな特殊能力まで身につけられる設定って、やりすぎでしょ!

ディノ
設定作ったの誰でしたっけ〜〜〜?

Lukia

ディノ
皆さま、白亜紀と数学のコラボ、末永くおつきあいください。m(_ _)m
[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません