高校数学の絶対値の問題は、グラフでイメージしよう。(その9)

[mathjax]
自宅のパソコンでブログ記事を書いていたはずが、
突然不思議な世界に迷い込み、
高校生?恐竜、ディノさんと出会ってしまった私。
ディノさんは、絶対値の問題の解き方を教えてくれたら、ひらけた場所までの案内をしてくれると言いますが・・・
さて、今日の問題の「解法」で、ディノさんは私を「解放」してくれるのでしょうか。
![]()
夕方になり、ご近所のお友達やチビ恐竜たちは、おうちに帰っていきました。
後片付けを手伝いながら、ディナさんとお話しをしていると・・・

ディノ
ディノさんの雄たけびは、勉強部屋どころか、近所にとどろいたため、
街路樹に止まっていた鳥?たちがバサバサと羽音を立てて逃げ出しました。

ディナ
ご近所に迷惑だろッ!

Lukia
ディナさん、ちょっと様子を見てきますね。

ディナ
片付けは私だけでも大丈夫だから、行ってやって。

Lukia
では、行ってきます。
そして、ディノさんの部屋に行ってみると。

ディノ

Lukia
ということは、式自体で、\(x\)が三つあるということですか?

ディノ

Lukia
じゃ、やってみましょう。
問題
$$\Large \color{blue}{\vert x \vert}+\color{red}{\vert x-4 \vert}=x+2$$
簡単な図を描こう。

Lukia
というわけで、相変わらずこの図が使えますから、描いておきましょうね。
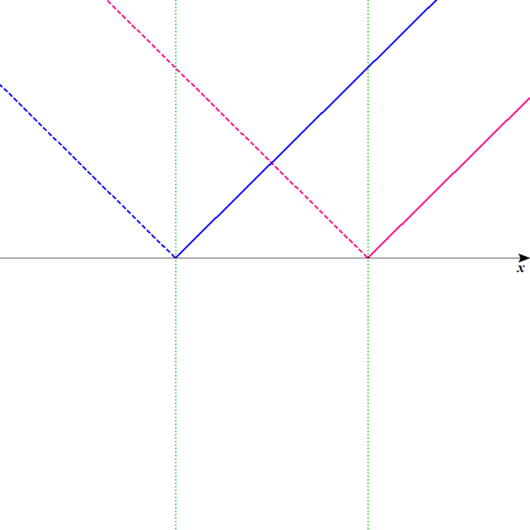
範囲を設定しよう。

ディノ
まずは、左辺にある二つの絶対値をなんとかしてから、
右辺との関係を見ていけばよかったんだよな。

Lukia
なんで、テンパっちゃったんでしょうねぇ。
というわけで、ディノさん、二つの絶対値の式が、それぞれ\(x\)軸と交わるときを求めてください。

ディノ
\(\color{blue}{\vert x \vert=0}\)となるのは、
\(x=\color{blue}{0}\)のときで、
\(\color{red}{\vert x-4 \vert=0}\)となるのは、
\(x=\color{red}{4}\)のときだ。

Lukia
図には以下のように書き込めますね。
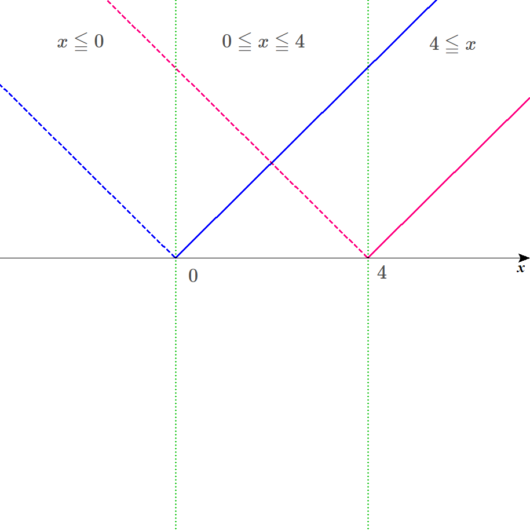
範囲ごとに式を書き込んでいく。

ディノ
\(\color{blue}{y=\vert x \vert}\)は、
\(y=\color{blue}{-x}\) \(\left( \color{blue}{x \leq 0} のとき\right)\)
\(y=\color{blue}{x}\) \(\left( \color{blue}{0 \leq x} のとき\right)\)と書き表すことができて、

ディノ
\(y=\color{red}{-x+4}\) \(\left( \color{red}{x \leq 4} のとき\right)\)
\(y=\color{red}{x-4}\) \(\left( \color{red}{4 \leq x} のとき\right)\)と書き表せる。

Lukia
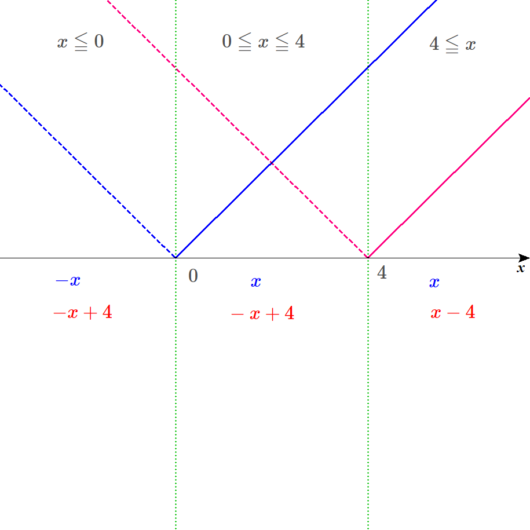
筆算する。

Lukia
今回の問題も、二つの絶対値が+(プラス)でつながっているから、たし算の筆算をすればいいですよね。

ディノ
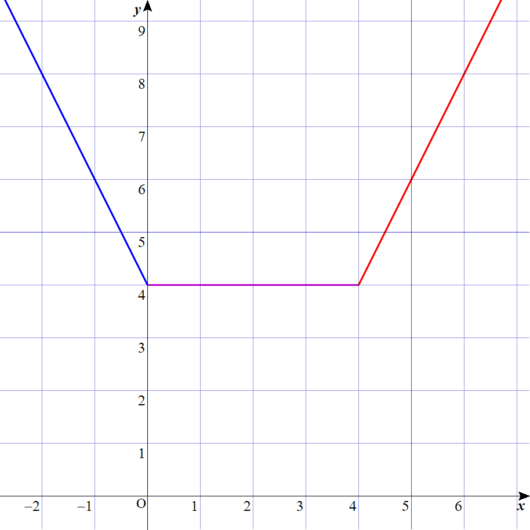
だから、それぞれの筆算の結果は、
左が、\(-2x+4\)
真ん中が、\(4\)
右が \(2x-4\)になる。
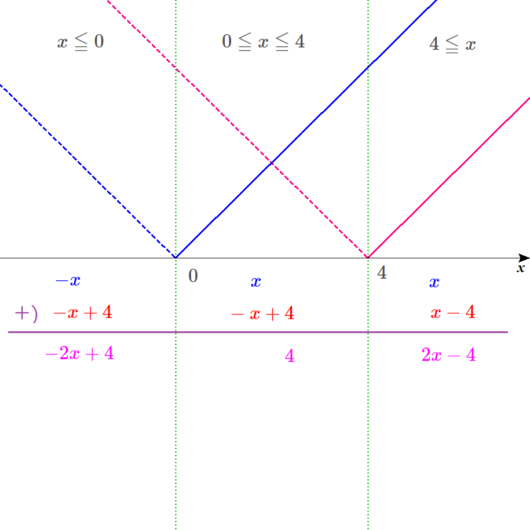
グラフを描くとこうなる。

Lukia
方程式を解く。

Lukia
いよいよ、=x+2 をつけて、方程式を解いてみましょう。

ディノ

Lukia
これまでの問題は、右辺が定数でしたけど、
今回の問題は、\(x\)が加わっているだけです。
左辺の絶対値をはずす工夫さえできれば、ただの一次方程式になっちゃうんですよね。

ディノ
案外なんてことない問題だったわけだな。
じゃ、左の範囲から、方程式を解いていくぞ。
左の範囲は、\(-2x+4=x+2\)を解いて、
\(x=\frac{2}{3}\)

ディノ
\(x=2\)

ディノ
\(x=6\)だ。

範囲を比較して答えを出す。

Lukia
左の範囲の解は、青い四角で囲み、\(x\)軸には、青い矢印で、だいたいの位置を示します。
真ん中の範囲の解は、紫の四角で囲み、\(x\)軸には、紫の矢印で、だいたいの位置を示します。
右の範囲の解は、赤い四角で囲み、\(x\)軸には、赤い矢印で、だいたいの位置を示します。
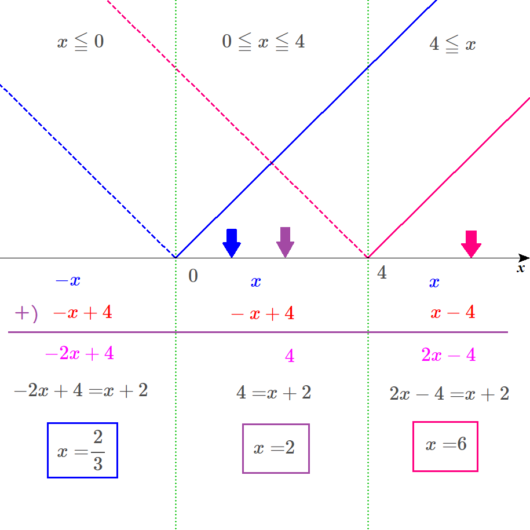

ディノ
ということは、\(x=\frac{2}{3}\)は不適。ということになるな。

Lukia
こたえ
$$\Large \vert x \vert+\vert x-4 \vert=x+2$$
$$\Large x=2 , x=6$$
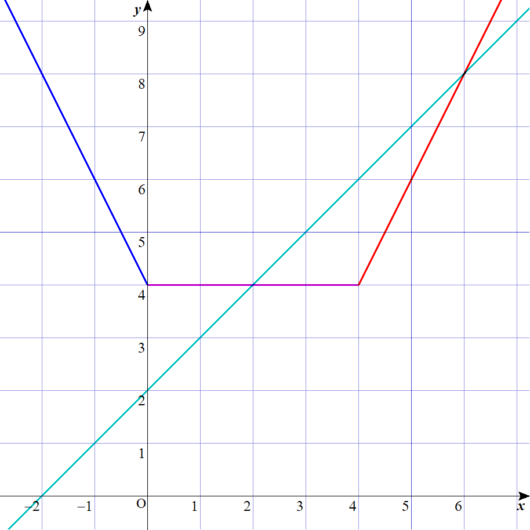

Lukia
\(y=x+2\)を描き加えたのが、上の図です。
緑の線が、\(y=x+2\)なのですが、やっぱり、青いグラフとは交わっていませんね。

ディノ
右辺の\(x\)ぐらいで、大騒ぎして、オレ恥ずかしいよ。

Lukia
ですから、あんまり恥ずかしがる必要はないですよ。

ディノ
やっぱ、オレ、すげぇかも。

Lukia
食べるか、解くかしかしていない。

ディナ
ごはんだよ~!

Lukia
そして、ばんごはんまで?

ディナ

Lukia

ディノ
で、かーちゃん、ばんごはん何?

ディノ

ディノ

Lukia


ディナ
なんてったって、女はチーズが好きなんだから♪

Lukia

ディナさんは、ディノさん向けのお肉がたっぷり入ったピザも作っていましたが、
私には、シンプルなマルゲリータを焼いてくれました。
さすが、カリスマ主婦。
手際がいいんだなぁ。
[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません