高校数学の「空間ベクトルとその内分比」に関する問題を解いてみる。（Yahoo!知恵袋より）

2019年1月5日2023年1月14日ベクトル実用数学技能検定（数学検定 数検),数検2級,数検準1級

[mathjax]

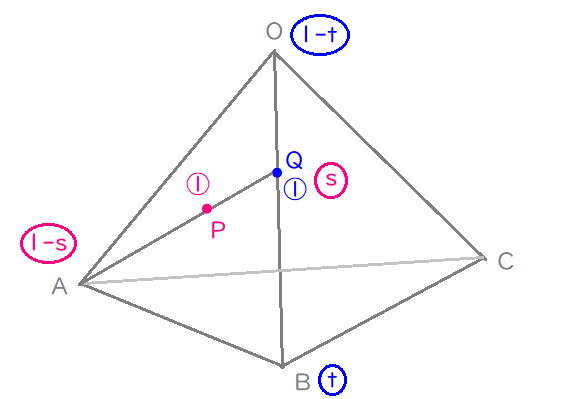
図を描いてイメージすることがだいじ。

まずは、簡単でいいので、空間図形を描いて、内分点を統一できるかどうか確かめてみましょう。

Lukia

点\(\mathrm{Q}\)において、青い文字で書いた内分比と、ピンクの文字で書いた内分比が重なっていますね。それぞれ互い違いにかけ算することによって、空間図形全体における内分比を統一することができます。

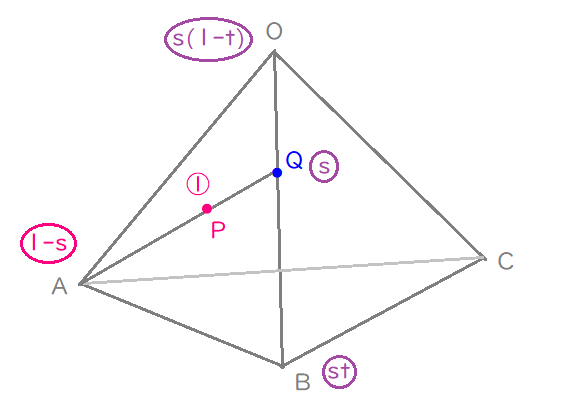
(1)を解く。

$$\begin{align}\overrightarrow{\mathrm{CP}}=&\overrightarrow{\mathrm{OP}}-\overrightarrow{\mathrm{OC}} \\\\ =&s\overrightarrow{\mathrm{OQ}}+\left( 1-s\right)\overrightarrow{\mathrm{OA}}-\overrightarrow{\mathrm{OC}} \\\\ =&s\cdot \frac{t}{s}\overrightarrow{\mathrm{OB}}+\left( 1-s\right)\overrightarrow{\mathrm{OA}}-\overrightarrow{\mathrm{OC}}\\\\ =&\left( 1-s\right)\overrightarrow{a}+st\overrightarrow{b}-\overrightarrow{c}\end{align}$$

(2)を解く。

Lukia

\(\overrightarrow{\mathrm{CP}}\)と平面\(\mathrm{OAB}\)と垂直であるということは、\(\overrightarrow{\mathrm{CP}}\)と\(\overrightarrow{a}\)と\(\overrightarrow{b}\)がそれぞれ垂直であるといえます。
それを数学的に表して、\(s \ , \ t\)に関する連立方程式を解けばよいことになりますね。

$$\begin{align}\overrightarrow{a}\cdot \overrightarrow{\mathrm{CP}}=&0 \\\\ \left( 1-s\right) +\frac{1}{2}\cdot st-\frac{1}{2}=&0\\\\ 2\left( 1-s\right)+st=&1\quad \quad \cdots\cdots① \end{align}$$

$$\begin{align}\overrightarrow{b}\cdot \overrightarrow{\mathrm{CP}}=&0 \\\\ \frac{2}{3}\cdot \left( 1-s\right)+st-\frac{1}{2}=&0 \\\\ 4\left( 1-s\right)+6st-3=&0\\\\ 4\left( 1-s\right)+6st=&3\quad \quad \cdots\cdots② \end{align}$$

$$\begin{align}②-2\times ①& \\\\ 4\left( 1-ｓ\right)+6st=&3 \\\\ -4\left( 1-s\right)-2st=&-2\\\\ 4st=&1\\\\ st=&\frac{1}{4} \\\\ \\\\ これを&①に代入する.\\\\ 2\left( 1-s\right)+\frac{1}{4}=&1\quad を計算して,\\\\ s=&\frac{5}{8}\\\\ t=&\frac{2}{5} \end{align}$$

(3)を解く。

$$\begin{align}\triangle \mathrm{OAB} \ の面積 \ \mathrm{S} \ とする.& \\\\ \mathrm{S}=&\frac{1}{2}\sqrt{1^2\cdot 1^2-\left( \frac{2}{3}\right)^2}=\frac{\sqrt{5}}{6} \end{align}$$
$$\begin{align}\vert \overrightarrow{\mathrm{CP}} \vert^2=&\vert \frac{3}{8}\overrightarrow{a}+\frac{1}{4}\overrightarrow{b}-\overrightarrow{c} \vert^2 \\\\ =&\frac{45}{16}\quad より \\\\ \vert \overrightarrow{\mathrm{CP}} \vert=&\frac{3\sqrt{5}}{4} \end{align}$$
$$四面体\mathrm \ {OABC} \ の体積を \ \mathrm{V} \ とする.$$
$$\begin{align}\mathrm{V}=&\frac{1}{3}\times \frac{\sqrt{5}}{6}\times \frac{3\sqrt{5}}{4} \\\\ =&\frac{5}{24} \end{align}$$

こたえ

$$\begin{align}\left( 1\right)\quad \overrightarrow{\mathrm{CP}}=&\left( 1-s\right)\overrightarrow{a}+st\overrightarrow{b}-\overrightarrow{c} \\\\ \left( 2\right)\quad \ s=&\frac{5}{8} \ , \ t=\frac{2}{5} \\\\ \left( 3\right)\quad \mathrm{V}=&\frac{5}{24} \end{align}$$

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。