高校数学の「平面ベクトル（比較的やさしい）」に関する問題を解いてみる。（Yahoo!知恵袋より）

2019年1月4日2023年1月14日ベクトル実用数学技能検定（数学検定 数検),数検2級,数検準1級

[mathjax]

準備をしよう。

Lukia

三角形を描き、情報を書き込んでいくとともに、
\(\overrightarrow{\mathrm{AE}}\)を\(\overrightarrow{\mathrm{AC}}\)を用いて表したり、
内積\(\overrightarrow{\mathrm{AB}}\cdot \overrightarrow{\mathrm{AC}}\)を求めておきましょう。

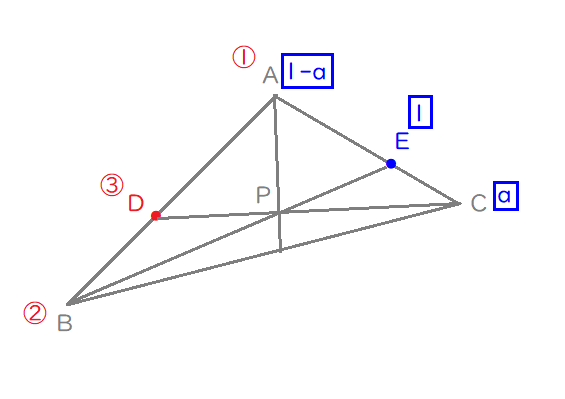
$$\overrightarrow{\mathrm{AE}}=a\overrightarrow{\mathrm{AC}}$$
$$\begin{align}\frac{\overrightarrow{\mathrm{AB}}\cdot \overrightarrow{\mathrm{AC}}}{\vert \overrightarrow{\mathrm{AB}} \vert\vert \overrightarrow{\mathrm{AC}} \vert}=&\cos \angle \mathrm{BAC} \\\\ \frac{\overrightarrow{\mathrm{AB}}\cdot \overrightarrow{\mathrm{AC}}}{2\sqrt{6}}=&\frac{2^2+\left( \sqrt{6}\right)^2-\left( \sqrt{10}\right)^2}{2\cdot 2\sqrt{6}}=0 \\\\ \overrightarrow{\mathrm{AB}}\cdot \overrightarrow{\mathrm{AC}}=&0 \end{align}$$
さらに，
$$\overrightarrow{\mathrm{AB}}\cdot \overrightarrow{\mathrm{AE}}=\overrightarrow{\mathrm{AB}}\cdot a\overrightarrow{\mathrm{AC}}=a\overrightarrow{\mathrm{AB}}\cdot \overrightarrow{\mathrm{AC}}=0$$

(1)を解く。

Lukia

頂点\(\mathrm{A}\)が2通りの内分比で示されているので、
内分比を統一していきます。
すると、下の図の紫色の文字で示す新たな内分比が示されます。

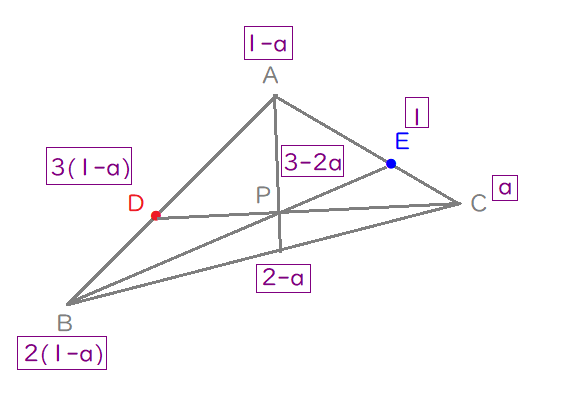
$$\begin{align}\overrightarrow{\mathrm{AP}}=&\frac{1}{3-2a}\lbrace 2\left( 1-a\right)\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AE}}\rbrace \quad より\\\\ t=&\frac{1}{3-2a} \end{align}$$

(2)を解く。

$$\begin{align}線分\mathrm{}は,&線分\mathrm{}と垂直に交わっているといえるので, \\\\ \overrightarrow{\mathrm{AP}}\cdot \overrightarrow{\mathrm{BE}}=&0\end{align}$$

(3)を解く。

(2)より,
$$\begin{align}\overrightarrow{\mathrm{AP}}\cdot \overrightarrow{\mathrm{BE}}=&0\\\\ \frac{1}{3-2a}\lbrace 2\left( 1-a\right)\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AE}}\rbrace\cdot \left( \overrightarrow{\mathrm{AE}}-\overrightarrow{\mathrm{AB}}\right)=&0\end{align}$$
$$\begin{align}ここで,\quad 1 \lt &3-2a \lt 3\quad であるから \\\\ 両辺を \ \left( 3-2a\right)&倍する.\end{align}$$
$$\begin{align}2\left( 1-a\right)\overrightarrow{\mathrm{AB}}\cdot \overrightarrow{\mathrm{AE}}+\vert \overrightarrow{\mathrm{AE}} \vert^2-2\left( 1-a\right)\vert \overrightarrow{\mathrm{AB}} \vert^2-\overrightarrow{\mathrm{AB}}\cdot \overrightarrow{\mathrm{AE}}=&0 \\\\ \overrightarrow{\mathrm{AB}}\cdot \overrightarrow{\mathrm{AE}}=&0\quad より\\\\ 6a^2+8a-8=&0\\\\ 3a^2+4a-4=&0\\\\ \left( a+2\right)\left( 3a-2\right)=&0\\\\ a=-2\quad ,\quad a=\frac{2}{3}&\\\\ 0 \lt a \lt 1 \ より& \ a=\frac{2}{3} \end{align}$$

こたえ

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。