高校数学の「絶対値・二次関数・不等式」に関する問題を解いてみる。（Yahoo!知恵袋より）

2018年12月20日2023年1月14日二次関数実用数学技能検定（数学検定 数検),数検準2級

[mathjax]

絶対値は内側からはずそう。

Lukia

絶対値記号の中に　さらに絶対値記号が含まれているような式の場合、
まずは内側の絶対値記号をはずしてみることからやってみましょう。
その際、\(x\)の範囲がのちのち影響するので、意識しておいてください。

$$\begin{align}y=&f\left( x\right) \ とし, \\ g\left( x\right)=&\vert x^2-2x \vert \ とする.\end{align}$$
$$\begin{align}x \leq 0 \ , \ 2 \leq x \ のとき,\quad \quad &g\left( x\right)=x^2-2x\cdots① \\ 0 \lt x \lt 2 \ のとき,\quad \quad &g\left( x\right)=-x^2+2x\cdots②\end{align}$$

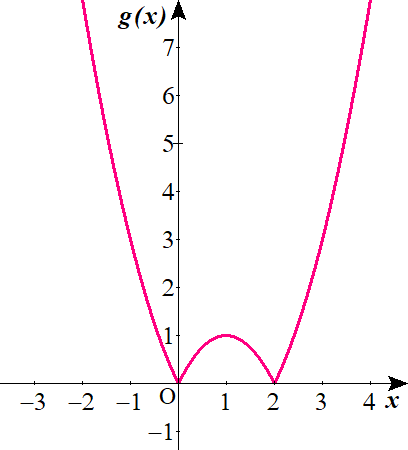
①, ②より
$$\begin{align}x \leq 0 \ , \ 2 \leq x \ のとき,\quad \quad &f\left( x\right)=\vert x^2-2x-3 \vert\cdots① \\ 0 \lt x \lt 2 \ のとき,\quad \quad &f\left( x\right)=\vert -x^2+2x-3 \vert\cdots②\end{align}$$

①を考える。

$$\begin{align}f\left( x\right)=\vert x^2-2x-3 \vert \ は&\\ x \leq -1 \ , \ 3 \leq x \ のとき\quad \quad &f\left( x\right)=x^2-2x-3 \\ -1 \lt x \lt 3 \ のとき\quad \quad &f\left( x\right)=-x^2+2x+3\\\end{align}$$

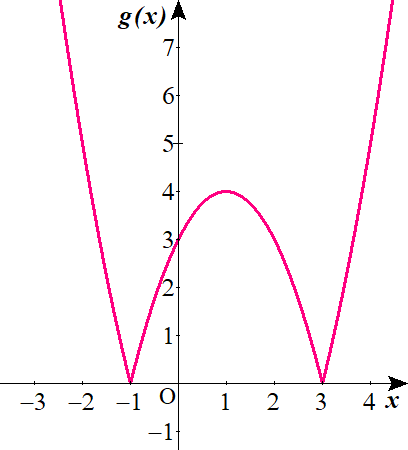
$$\begin{align} \\ただし \ x \leq 0 \ , \ 2 \leq x \ であるので,\\ x \leq -1 \ , \ 3 \leq x \ のとき\quad \quad &f\left( x\right)=x^2-2x-3\\ -1 \lt x \leq 0 \ , \ 2 \leq x \lt 3 \ のとき\quad \quad &f\left( x\right)=-x^2+2x+3\end{align}$$

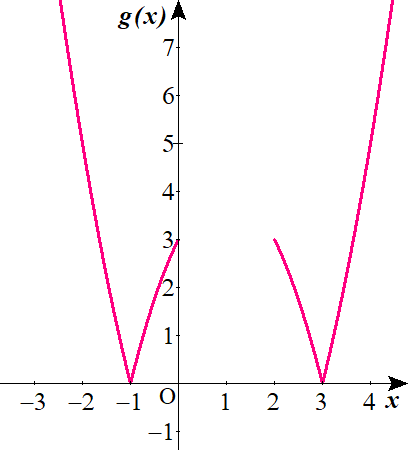
②を考える。

Lukia

①を詳しく解くことで、上の画像のようなグラフが描けました。
しかし、\(0 \leq x \leq 2\)の範囲がぽっかり空いていますね。
②がそこを埋めることになるのですが、ちょっと難しいです。

$$\begin{align}xに関する2次方程式 \ &-x^2+2x-3=0 \ において \ その判別式を\mathrm{D} \ とする. \ \\ \mathrm{D}=&4-12=-8 \lt 0 \ より \\ y=-x^2+2x-3 \ は,\quad &x軸と交わらない \ 上に凸の関数である. \end{align}$$

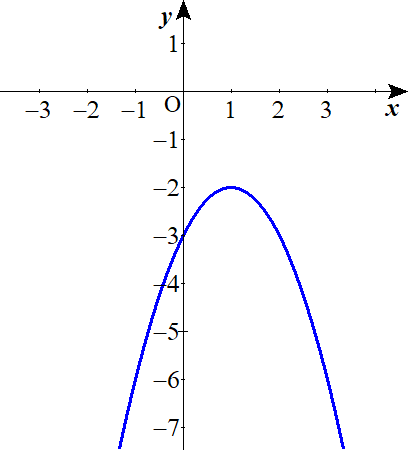
Lukia

ということは、このグラフを\(x\)軸でパタンと折り返せばいいことになりますね。

まとめて（場合分けをして）、グラフを描く。

$$\begin{align}0 \lt x \lt 2 \ のとき\quad \quad f\left( x\right)=&\vert -x^2+2x-3 \vert \\ =&x^2-2x+3 \\ =&\left( x-1\right)^2+2 \end{align}$$
$$\begin{align}① \ , \ ② \ より& \\ f\left( x\right)=&x^2-2x-3\quad \quad x \leq -1 \ , \ 3 \leq x \ のとき \\ f\left( x\right)=&-x^2+2x+3\quad \quad -1 \lt x \leq 0 \ , \ 2 \leq x \lt 3 \ のとき\\ f\left( x\right)=&x^2-2x+3\quad \quad 0 \lt x \lt 2 \ のとき \end{align}$$

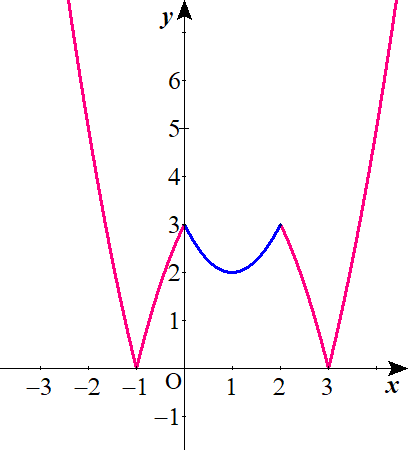
なるべく正確なグラフを描く。

Lukia

グラフを利用して、不等式を解け。ということですから、
できるだけ正確なグラフを描くようにしましょう。
学校の定期テストなどで、このような問題が出された場合は、グラフが描きやすいよう、格子線が引かれた解答欄が設けられているかもしれません。
しかし、大学の二次試験などの解答用紙は、白紙ですし、大学入試センター試験に至っては、ものさしの持ち込みが禁止されているので、定期テストのような親切な解答用紙は期待できません。
日ごろからフリーハンドで、均等に点が打てる、格子線が引ける練習をしておくとよいでしょう。

Lukia

(1)で作成したグラフに、
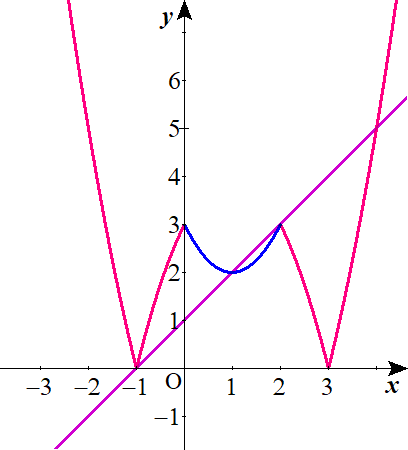
\(y=x+1\)を紫色の直線で示します。

Lukia

赤と青の曲線よりも紫色の直線が下にある範囲を求めればよいことになります。

$$グラフより\quad x \leq 1$$

こたえ

(1)

(2)
$$x \leq 1$$

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。