高校数学の「絶対値を含む二次関数とその共有点」に関する問題を解いてみる。（Yahoo!知恵袋より）

2018年11月20日2023年1月14日二次関数実用数学技能検定（数学検定 数検),数検準2級

[mathjax]

ディノ

うおぉ！式の一部に絶対値が含まれてるぞ～～～！

Lukia

ディノさん、ひとまず食べちゃってから解きませんか？
見た感じ、少し時間がかかるので、溶けちゃいますよ？

ディノ

お、そうか。じゃすぐ食っちゃおうぜ♪

ディノさんは、その後一口でアイスクリームを食べてしまいました。
私は、もう少しのんびり食べたかったのにな・・・。

絶対値をはずして、グラフを描こう。

Lukia

では、ディノさん、まずすることはなんですか？

ディノ

そりゃぁ、絶対値をはずすことだよ。

Lukia

そうですね。ではさっそくやってみましょう。

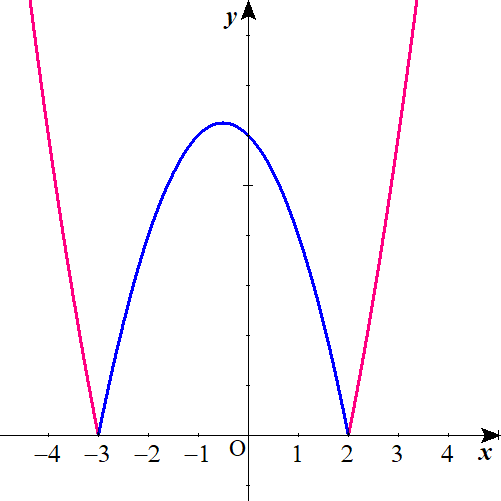
$$\begin{align}f\left( x\right)=&\vert x^2+x-6 \vert \ とする。 \\\\ f\left( x\right)=&x^2+x-6\quad \left( x \leq -3 \ , \ 2 \leq x\right) \\\\ f\left( x\right)=&-x^2-x+6\quad \left( -3 \leq x \leq 2\right) \end{align}$$

Lukia

グラフは、以下の通りになりますね。

ディノ

ということは、もともとの\(y=\cdots\)の式も、青のグラフのときと、ピンクのグラフのときじゃ違ってくるってことだよな。

Lukia

おっ、なかなかカンがいいですね。
では、書き直してみてくれますか？

$$\begin{align}&x \leq -3 \ , \ 2 \leq x\quad のとき\\\\ y=&\color{#f700ca}{x^2+x-6}+x\\\\ =&x^2+2x-6\\\\ =&\left( x+1\right)^2-7 \end{align}$$
$$\begin{align}&-3 \lt x \lt 2\quad のとき \\\\ y=&\color{#0004fc}{-x^2-x+6}+x \\\\ =&-x^2+6 \end{align}$$

Lukia

これらの式をもとにグラフを描くと、
以下のようになります。

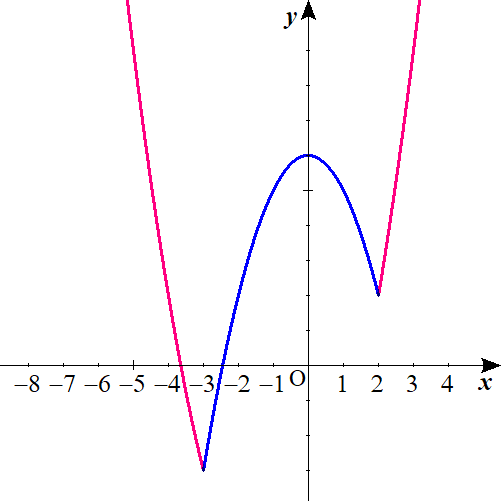
直線y=aとの共有点を探す。

Lukia

\(y=a\)の\(a\)は、実数であればなんでもいい。という意味になります。
ちなみに、\(x\)と\(y\)のどちらの軸に平行ですか？

ディノ

ええっと・・・
（たとえば\(y=3\)として・・・）
おっ、\(x\)軸に平行だな！

Lukia

そうです。それでは、先ほどのグラフに、ものさしなどをあてて、共有点の個数を探していきましょう。
ちなみに、問題では、「共有点が3つになるとき」とありますから、ものさし\(\left( y=a\right)\)とグラフが3点で交わるときを探せばいいですね。

私がそういうと、ディノさんは、ものさしをグラフにあてて、上下にスライドさせました。

ディノ

グラフ自体が、\(y=-3\)より下にはないから、そこから上にスライドさせてみるぞ。
おっ、\(y=-3\)のときは、1点だったが、さっそく2点で交わってるな。
あっ、\(y=2\)のとき、3点になった！

Lukia

もうなさそうですか？

ディノ

いや、グラフはまだ続いてるんだから、まだスライドしてみるぞ。
\(y=2\)を過ぎたとたん、4つになった。
このまま4つなのか？
・・・
いや、また3点になった！\(y=6\)のときだ！
そして、それ以降はずっと2点だな。

Lukia

つまり、グラフと\(y=a\)が3点で交わるのは、
\(a=6\)のときと、
\(a=2\)のとき。ということになりますね。

場合分けをしてこたえを求める。

$$\begin{align}ⅰ）&a=2 \ のとき \\\\ &2=\color{#f700ca}{x^2+2x-6} \quad \left( x \leq -3 \ , \ 2 \leq x\right)\\\\ &x^2+2x-8=0 \\\\ &x=-4 \ , \ 2 \\\\ &2=\color{#0004fc}{-x^2+6}\quad \left( -3 \leq x \leq 2\right) \\\\ &x^2-4=0\\\\ &範囲より \ x=-2\ \\\\ &以上より、a=2 \ のときの共有点は\\\\ &x=-4 \ , \ -2 \ , \ 2 \end{align}$$

$$\begin{align}ⅱ）&a=6 \ のとき \\\\ &6=\color{#f700ca}{x^2+2x-6} \quad \left( x \leq -3 \ , \ 2 \leq x\right)\\\\ &x^2+2x-12=0\\\\ &x=-1 \pm \sqrt{13}\ \\\\ &6=\color{#0004fc}{-x^2+6}\quad \left( -3 \leq x \leq 2\right)\\\\ &x^2=0\\\\ &x=0\ \\\\ &以上より、a=6 \ のときの共有点は\\\\ &x=-1 \pm \sqrt{13} \ , \ 0\end{align}$$

こたえ

$$\begin{align}ⅰ）&a=2 \ のとき\\\\ &x=-4 \ , \ -2 \ , \ 2\ \\\\ ⅱ）&a=6 \ のとき\\\\&x=-1 \pm \sqrt{13} \ , \ 0 \end{align}$$

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。