中学数学の「列車−鉄橋」に関する問題を解いてみる。(Yahoo!知恵袋)

2020年5月22日2023年1月13日列車トンネル問題実用数学技能検定（数学検定数検),数検3級

読了時間: 約3分55秒

問題

[mathjax]長さ\( \ 160m\ \)の列車が時速\( \ 72km\ \)で走っている。この列車の長さが\( \ 560m\ \)の鉄橋を渡り始めてから渡り終わるまでにかかる時間は何秒か。

解法

今からあなたは身長160mの超巨人です。

「鉄橋を渡りきる」だとか、「トンネルを通り抜ける」という問題がありますが、
列車を擬人化（ぎじんか）できるかどうかにかかっていると思います。
もっというと、「列車=あなた」というイメージができるかどうか。

今から、あなたは身長\( \ 160m\ \)の超大型巨人です。
あなたの身長ぴったりに作られた列車があり、あなたはその専用列車に横たわった状態で移動します。

鉄橋を渡るということは。

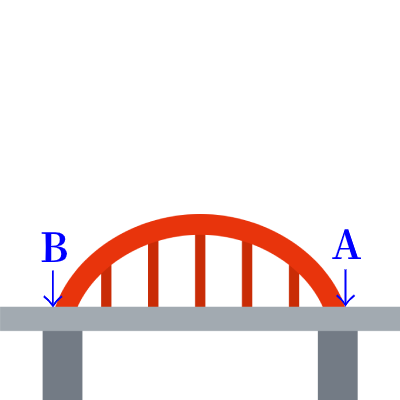
上に示したイラストは、鉄橋のイメージ画像です。（K-factoryさん@イラストAC）
身長160mのあなたは、今からこのAB区間を通り抜ける時間を計ります。

さて、まずは「計りはじめ」を確認しましょう。
計測者は、あなたの体のどの部位がA地点と重なった時にストップウォッチのスタートボタンを押せばよいでしょうか。

正解は、「頭頂部（頭の先）がA地点と重なった時」ですね。
くどいようですが、A地点よりも右側でボタンを押すと、「まだ橋を渡りはじめていない」ことになりますし、
A地点を過ぎ、あなたの鼻がA地点と重なるときにボタンを押すと、「すでに渡りはじめている」ことになってしまいます。
あなたの頭のてっぺんがA地点とぴったり重なって見える瞬間にボタンを押さなければ、正確な時間を計測できません。

次は、もう少し難しいです。ここが「列車−鉄橋（またはトンネル）」問題のキモではないでしょうか。

それでは、計り終わり、すなわちストップウォッチのストップボタンを押すのはどのタイミングでしょうか。

「頭のてっぺんがB地点と重なったとき」？
これだと、B地点を通過したのは、「頭のてっぺん」だけで、あなたの顔も体も足先も、まだまだ鉄橋に隠れて全体が見えませんね。

あなたの体が鉄橋にまったく隠れていない状態とは、
「足先とB地点が重なったとき」です。

「鉄橋を渡りきる」ということは、
「頭のてっぺんから徐々に鉄橋に隠れていき、再び足先が見えるようになるまでレール上を移動する」ということを表しています。

足先が完全に見えるまで、頭のてっぺんが移動する距離は？

鉄橋に隠れていた身長160mのあなたの足先が、再び見えるようになるには、
頭のてっぺんは、どれだけ移動しなければならないでしょうか。

再度、鉄橋のイメージ画像を示します。
あなたの足先がB地点と重なるためには、頭のてっぺんは、B地点よりも左に何m移動する必要があるでしょうか。

あなたの身長は160mなのですから、B地点よりも160m離れていなければなりませんね。
（短かったら、足や腰を曲げている可能性がありますし、もしB地点から180m左に移動していたら、鉄橋と足先は重なっていないことになります）

こうしてみると、「鉄橋をわたりきる」ため、あなたの頭のてっぺんは、
\( \ 560+160=720\left( m\right)\ \)移動する必要があることになりますね。

Lukia

今回求めるのは、「（鉄橋を渡りきるのにかかった）時間」ですから、
基本的には
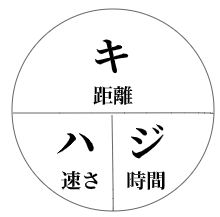
\( \ \frac{距離}{速さ} \ \)にあてはめていけばよさそうですね。

\( \ \begin{align}時間=\frac{距離}{速さ}=&\frac{\left( 560+160\right)m}{72km/時間} \\\\ =&\frac{720m}{\frac{72km\cdot 1000m/km}{1時間\cdot 60分/時間}}=\frac{720m}{\frac{72000m}{60分}}=\frac{720\times 60分}{72000}\\\\ =&\frac{6}{10}分=\frac{6}{10}分\cdot 60秒/分\\\\ =&36秒 \end{align} \ \)

計算しながら単位も直していこう。

今回の問題の場合、「鉄橋を渡りきるまでにかかった時間中の移動距離」である\( \ 720m\ \)を\( \ 0.72km\ \)に直すほうが定石かもしれません。

\( \ \begin{align}\frac{720m}{72km/時間}=&\frac{0.72km\cdot 1時間}{72km} \\\\ =&\frac{1時間\cdot 60分/時間}{100} \\\\ =&\frac{60分}{100}=\frac{60分\cdot 60秒/分}{100}\\\\ =&\frac{3600秒}{100}\\\\ =&36秒 \end{align} \ \)

Lukia

小数点がついた計算だけでもややこしいのに、分数の計算って・・・。
私は間違える自信しかないので、小さい単位に直していく方を選びます。

違いとしては、
m(メートル）をkm（キロメートル）に直すか、
km（キロメートル）をm（メートル）に直すか。だけで、後はやることは同じです。
しかし、最終的に「秒」という小さな単位を求めていくので、
km（キロメートル）をm（メートル）に直していくほうが楽だろうと思います。

Lukia

また、計算式に単位を書いてよいかどうか。ということについては、
学校の先生に相談してみてください。
私は、単位だとわかるように（）カッコをつけたらいいんじゃないか。と思いますが、
「計算式に単位を書き込むなんて言語道断！」とか言われるなら、
それは直接教えてくださる先生のお考えに従うべきだろうと思います。

高校入試で、計算式に単位を書いて、値は正しいのにやり方が正しくなくて減点。
なんてことになったら、冴えません。