高校数学の「三角比と図形」に関する問題を解いてみる。（Yahoo!知恵袋より）

2018年11月13日2023年1月15日図形と計量実用数学技能検定（数学検定 数検),数検準2級

[mathjax]

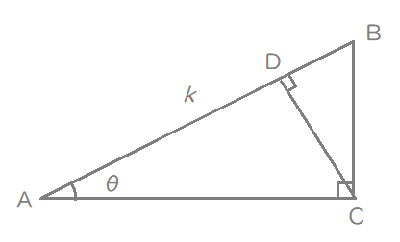
（1）上の直角三角形において、
$$\begin{align}\cos \theta=&\frac{\mathrm{AC}}{\mathrm{AB}} \ より \\\\ \mathrm{AC}=&k\cos \theta\end{align}$$

(2) 上の直角三角形において、
$$\begin{align}\sin \theta=&\frac{CD}{\mathrm{AC}} \ より、 \\\\ \mathrm{CD}=&\mathrm{AC}\cdot \sin \theta \\\\ =&k\sin \theta\cos \theta \end{align}$$

$$(3)\quad \triangle \mathrm{ABC} \sim \triangle \mathrm{CBD}より、$$
$$\begin{align}\angle \mathrm{BCD}=&\theta \ \\\\ \sin \theta=&\frac{\mathrm{BD}}{\mathrm{BC}}=\frac{\mathrm{BC}}{\mathrm{AB}} \\\\ \mathrm{AB}\cdot \mathrm{BD}=&\mathrm{BC}^2\\\\ =&k^2-k^2\cos^{2} \theta\\\\ k\mathrm{BD}=&k^2\left( 1-\cos^{2} \theta\right) \\\\ &k \gt 0 \ より\\\\ \mathrm{BD}=&k\sin^{2} \theta \end{align}$$

こたえ

$$\begin{align}\left( 1\right)\quad \mathrm{AC}=&k\cos \theta \\\\ \left( 2\right)\quad \mathrm{CD}=&k\sin \theta\cos \theta \\\\ \left( 3\right)\quad \mathrm{BD}=&k\sin^{2} \theta \end{align}$$

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。