高校数学の「軸が変数の放物線の最大・最小」に関する問題を解いてみる。(Yahoo!知恵袋より)

2021年11月25日2023年1月11日二次関数

Yahoo!知恵袋の高校数学カテゴリに掲載されていた「軸が変数の放物線の最大・最小」に関する問題を解いてみました。

解法

\( \ y=f\left( x\right) \ \)とする。
\( \ f\left( x\right)=\left( x-a\right)^2-a^2 \ \)
頂点は、\( \ \left( a \ , \ -a^2\right) \ \)である。
以下、①〜④におけるそれぞれの放物線とその軸、定義域の位置関係を示す。

① \( \ a \leqq 0 \ \) のとき

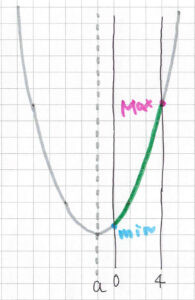最大値： \( \ f\left( 4\right)=4-4a \ \)
最小値： \( \ f\left( 0\right)=0 \ \)

② \( \ 0 \leqq a \leqq 2 \ \) のとき

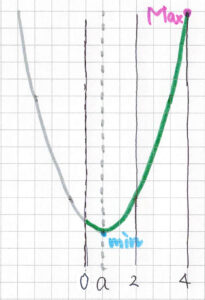最大値： \( \ f\left( 4\right)=4-4a \ \)
最小値： \( \ f\left( a\right)=-a^2 \ \)

③ \( \ 2 \leqq a \leqq 4 \ \) のとき

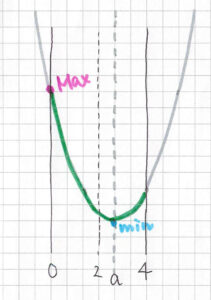最大値： \( \ f\left( 0\right)=0 \ \)
最小値： \( \ f\left( a\right)=-a^2 \ \)

④ \( \ 4 \leqq a \ \) のとき

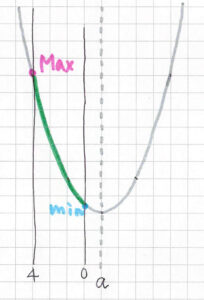最大値： \( \ f\left( 0\right)=0 \ \)
最小値： \( \ f\left( 4\right)=4-4a \ \)

こたえ

	①	②	③	④
最大値	\( \ 4-4a \ \)	\( \ 4-4a \ \)	\( \ 0 \ \)	\( \ 0 \ \)
最小値	\( \ 0 \ \)	\( \ -a^2 \ \)	\( \ -a^2 \ \)	\( \ 4-4a \ \)

Leave This Blank:Leave This Blank Too:Do Not Change This:

メールアドレス：