高校数学？の「人数と割合」に関する問題を解いてみる。(Yahoo!知恵袋より)
読了時間: 約1分32秒
問題
ある学年で英語と数学のテストを行った。
その結果、2科目とも合格した人の数は全体の\(\Large \frac{9}{16}\)、
各科目の不合格だった人の数は、英語が\( \ 11\ \)人、数学が全体の\(\Large \frac{5}{16}\)であった。
また、2科目とも不合格だった人の数は、数学が不合格だった人の数の\( \ 1\ \)割より少なかった。
（1） 全体の人数を\( \ x\ \)人とおき、2科目とも不合格だった人の数を\( \ x\ \)で表せ。
（2) \( \ x\ \)の値を求めよ。
解法
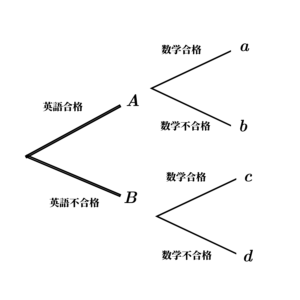
(1)
上の図のように各条件に該当する生徒の数をそれぞれ\( \ A,B,a,b,c,d\ \)とする。
\( \ B=11\ \),\( \ a=\ \)\(\Large \frac{9}{16}x\),\( \ b+d=\ \)\(\Large \frac{5}{16}x\)より、
\( \ c=\ \)\(\Large \frac{2}{16}x\)と表せる。
\( \ B=c+d\ \)より
$$\begin{align}11=&\frac{2}{16}x+d \\\\ d=&11-\frac{1}{8}x \end{align}$$
\( \ B=11\ \),\( \ a=\ \)\(\Large \frac{9}{16}x\),\( \ b+d=\ \)\(\Large \frac{5}{16}x\)より、
\( \ c=\ \)\(\Large \frac{2}{16}x\)と表せる。
\( \ B=c+d\ \)より
$$\begin{align}11=&\frac{2}{16}x+d \\\\ d=&11-\frac{1}{8}x \end{align}$$
(2)
\( \ d \gt 0\ \)より
$$\begin{align}d=&11-\frac{1}{8}x \gt 0\\\\ \frac{1}{8}x \lt &11 \\\\ x \lt &88 \end{align}$$
また、条件より
$$\begin{align}d \lt &\left( b+d\right)\times \frac{1}{10} \\\\ 10\left( 11-\frac{1}{8}x\right) \lt &\frac{5}{16}x \\\\ 22-\frac{1}{4}x \lt &\frac{1}{16}x \\\\ 22\times 16-4x \lt &x\\\\ 70.4 \lt &x \end{align}$$
まとめると
\( \ 70.4 \lt x \lt 88\ \)
ここで\( \ x\ \)は\( \ 16\ \)の倍数である必要がある。
よって\( \ x=80\ \)
$$\begin{align}d=&11-\frac{1}{8}x \gt 0\\\\ \frac{1}{8}x \lt &11 \\\\ x \lt &88 \end{align}$$
また、条件より
$$\begin{align}d \lt &\left( b+d\right)\times \frac{1}{10} \\\\ 10\left( 11-\frac{1}{8}x\right) \lt &\frac{5}{16}x \\\\ 22-\frac{1}{4}x \lt &\frac{1}{16}x \\\\ 22\times 16-4x \lt &x\\\\ 70.4 \lt &x \end{align}$$
まとめると
\( \ 70.4 \lt x \lt 88\ \)
ここで\( \ x\ \)は\( \ 16\ \)の倍数である必要がある。
よって\( \ x=80\ \)
$$80人$$共有:
プロフィール
Author Profile
