高校数学の「3つも絶対値が含まれた式の最小値」に関する問題を解いてみる。(Yahoo!知恵袋より)
読了時間: 約1分10秒
問題
[mathjax]\( \ f\left( x\right)=\vert x+1 \vert+\vert x-1 \vert+\vert x-2 \vert\ \)の最小値を求めよ。
解法
Lukia
絶対値が2つ含まれようが、3つ含まれようが、やることは同じです。
簡易のグラフを描いてわかりやすい場合分けの表を作成して考えましょう。
簡易のグラフを描いてわかりやすい場合分けの表を作成して考えましょう。
\( \ f\left( x\right)=g\left( x\right)+h\left( x\right)+k\left( x\right)\ \)とする。
ただし
\( \ g\left( x\right)=\vert x+1 \vert \ \)
\( \ h\left( x\right)=\vert x-1 \vert \ \)
\( \ k\left( x\right)=\vert x-2 \vert \ \)とする。
ただし
\( \ g\left( x\right)=\vert x+1 \vert \ \)
\( \ h\left( x\right)=\vert x-1 \vert \ \)
\( \ k\left( x\right)=\vert x-2 \vert \ \)とする。
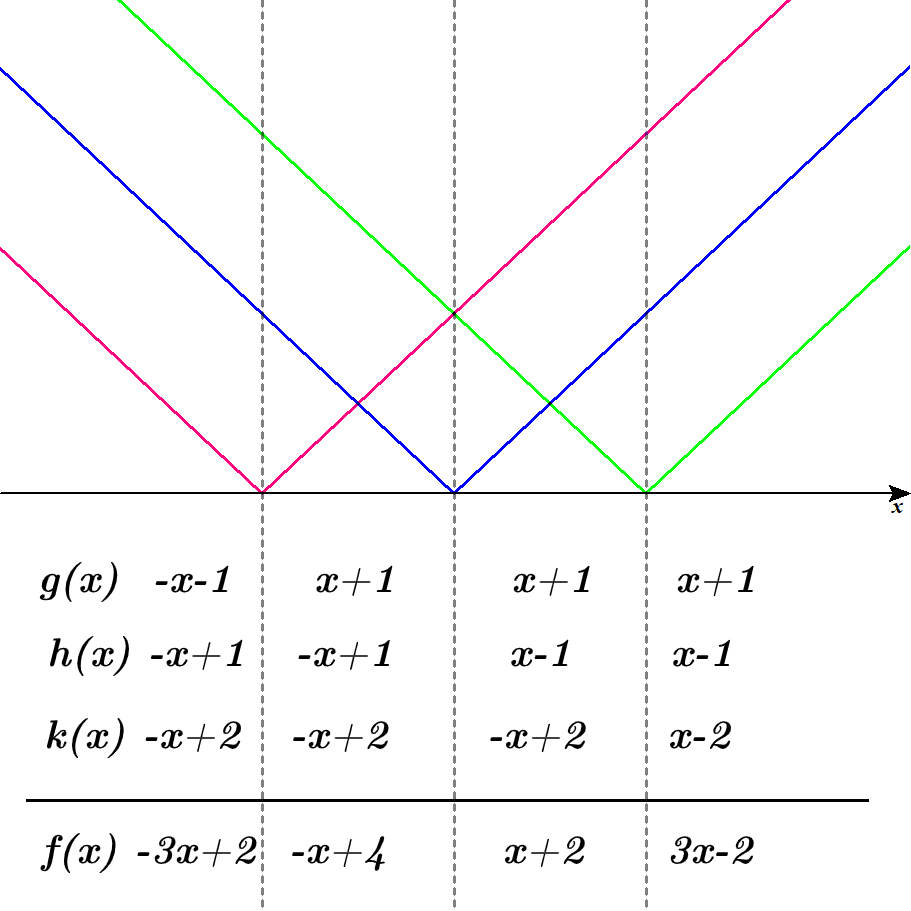
上の表より
\( \ f\left( x\right)=-3x+2\quad \left( x \lt -1\right)\ \)
\( \ f\left( x\right)=-x+4\quad \left( -1 \leq x \lt 1\right)\ \)
\( \ f\left( x\right)=x+2\quad \left( 1 \leq x \lt 2\right)\ \)
\( \ f\left( x\right)=3x-2\quad \left( 2 \leq x\right)\ \)
であり、グラフは以下のとおりとなる。
\( \ f\left( x\right)=-3x+2\quad \left( x \lt -1\right)\ \)
\( \ f\left( x\right)=-x+4\quad \left( -1 \leq x \lt 1\right)\ \)
\( \ f\left( x\right)=x+2\quad \left( 1 \leq x \lt 2\right)\ \)
\( \ f\left( x\right)=3x-2\quad \left( 2 \leq x\right)\ \)
であり、グラフは以下のとおりとなる。
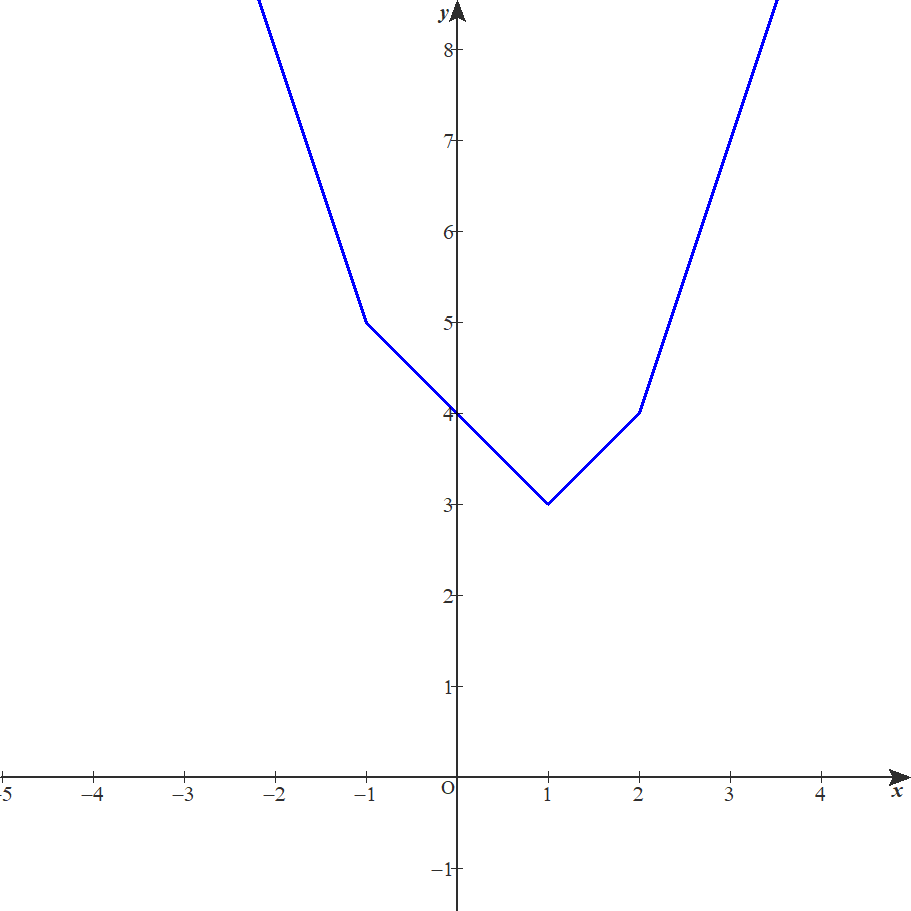
ゆえに求める最小値は\( \ 3\ \)
こたえ
最小値は 3
共有:
プロフィール
Author Profile