高校数学の「絶対値が含まれる式と定義域」に関する問題を解いてみる。（Yahoo!知恵袋より）
読了時間: 約1分59秒
[mathjax]
問題
\( \ f\left( x\right)=\vert 2x-1 \vert+\vert x+2 \vert\ \)において
\( \ -\frac{1}{2} \leq x \leq \frac{1}{2}\ \)のときの\( \ f\left( x\right)\ \)を\( \ x\ \)を用いて表わせ。
\( \ -\frac{1}{2} \leq x \leq \frac{1}{2}\ \)のときの\( \ f\left( x\right)\ \)を\( \ x\ \)を用いて表わせ。
解法
ディノ
うわ〜、久しぶりだぞぉ〜！
Lukia
ホントですねぇ。というか、ディノさん、見た目変わってません？
ディノ
おう。イメチェンしたんだ。(笑)
Lukia
ほぉ、イメチェン。(笑)
さて、今回は二つの絶対値が含まれる式について、ある定義域ではどんな式になるか。という問題です。
さて、今回は二つの絶対値が含まれる式について、ある定義域ではどんな式になるか。という問題です。
ディノ
定義域かぁ。難しいのか？
Lukia
まぁ、いつもどおり\( \ f\left( x\right)\ \)について場合分けをしていけば大丈夫だと思います。
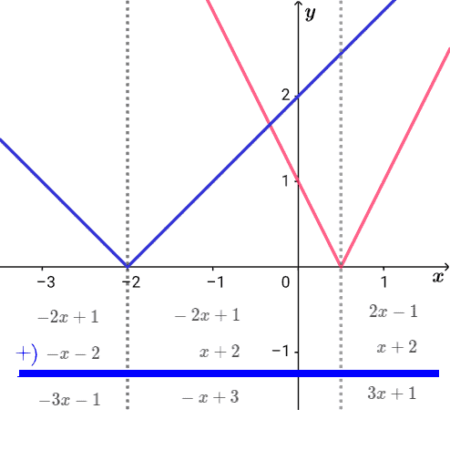
\( \ g\left( x\right)=\vert 2x-1 \vert\ \)とし、\( \ h\left( x\right)=\vert x+2 \vert\ \)とする。
\( \ f\left( x\right)=g\left( x\right)+h\left( x\right)\ \)と表せる。
\( \ \begin{align}g\left( x\right)=&2x-1\quad \left( \frac{1}{2} \leq x\right) \\\\ g\left( x\right)=&-2x+1\quad \left( x \lt \frac{1}{2}\right) \\\\ \\\\ h\left( x\right)=&x+2\quad \left( -2 \leq x\right) \\\\ h\left( x\right)=&-x-2\quad \left( x \lt -2\right) \end{align} \ \)
\( \ \begin{align}f\left( x\right)=&-2x+1-x-2=-3x-1\quad \left( x \lt −2\right) \\\\ f\left( x\right)=&-2x+1x+2=-x+3\quad \left( -2 \leq x \lt \frac{1}{2}\right) \\\\ f\left( x\right)=&2x-1+x+2=3x+1\quad \left( \frac{1}{2} \leq x\right) \end{align} \ \)
ゆえに求める\( \ f\left( x\right)=-x+3\ \)である。
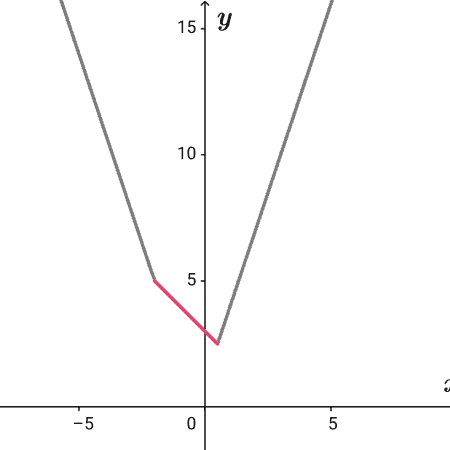
こたえ
\( \ f\left( x\right)=-x+3\ \)
共有:
プロフィール
Author Profile