高校数学の「底の変換公式を用いて対数の大きさを推定する」問題を解いてみる。(Yahoo!知恵袋より)

読了時間: 約3分23秒
[mathjax]
問題
次の不等式を満たす自然数\( \ n \ \)を求めなさい。
\( \ \frac{1}{n+1} \lt \log 2 \lt \frac{1}{n} \ \)
\( \ \frac{1}{n+1} \lt \log 2 \lt \frac{1}{n} \ \)
形をそろえよう

Lukia
指数・対数を学びはじめたばかりの人には、対数の考え方だけでもハードなのに、分数にはさんで自然数\( \ n \ \)を特定しろだなんて。
ひどいよねッ!しかし、そんなことを言っていても始まらないので、できることはないか、
どこかをいじって、楽ができないかを考えてみましょう。
ひどいよねッ!しかし、そんなことを言っていても始まらないので、できることはないか、
どこかをいじって、楽ができないかを考えてみましょう。

Lukia
いま、与えられている不等式をよく観察してみると、
両端の辺が分数になっていますね。
高校数学において、分数って厄介な存在です。
というのも、分数って早くは小学校の算数から出てくるのですから、単元特有のものとはいえません。
この問題は、指数・対数を学んでいるときに出てきた問題ですから、
対数をいじって、どうにか「形をそろえる」ことができないか。と考えます。
両端の辺が分数になっていますね。
高校数学において、分数って厄介な存在です。
というのも、分数って早くは小学校の算数から出てくるのですから、単元特有のものとはいえません。
この問題は、指数・対数を学んでいるときに出てきた問題ですから、
対数をいじって、どうにか「形をそろえる」ことができないか。と考えます。

Lukia
\( \ \log 2 \ \)とは、\( \ \log_{10}2 \ \)のこと。
底の変換公式を用いて、両端の辺と同じように「分数」の形(特に\( \ \frac{1}{対数} \ \)の形)にできないかを考えます。
底の変換公式を用いて、両端の辺と同じように「分数」の形(特に\( \ \frac{1}{対数} \ \)の形)にできないかを考えます。
$$\begin{align}\log 2& について底の変換公式を用いる\\\\ \log_{10}2=&\frac{\log_{2}2}{\log_{2}10}=\frac{1}{\log_{2}10} \\\\ ゆえに与式は\ &\frac{1}{n+1} \lt \frac{1}{\log_{2}10} \lt \frac{1}{n} \end{align}$$

Lukia
指数・対数の単元で「底の変換公式」を使いこなす練習は必ずあるので、
ちょっとずるいかもしれないのですが、(底の変換公式が使えないかな?)という発想は必要ですね。
こうして、底の変換公式を用いたことで、いわば整数型だった対数が、分数型の対数に変形できました。
あとは、分母だけを見ていけばよさそうです。
ちょっとずるいかもしれないのですが、(底の変換公式が使えないかな?)という発想は必要ですね。
こうして、底の変換公式を用いたことで、いわば整数型だった対数が、分数型の対数に変形できました。
あとは、分母だけを見ていけばよさそうです。
逆数にして自然数を推定する

Lukia
それでは、いよいよ\( \ \log_{2}10 \ \)の大きさについて考えてみましょう。
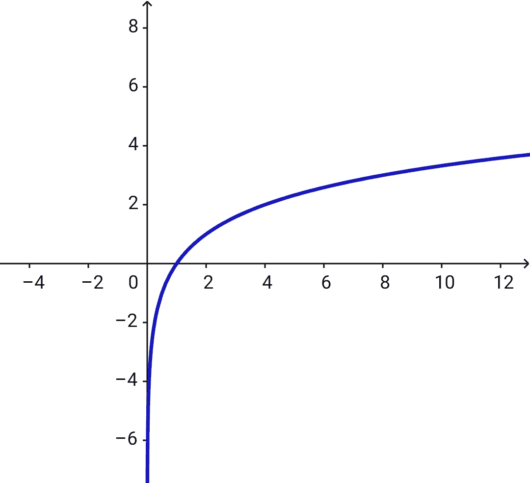
ちなみに、\( \ y=\log_{2}x \ \)のグラフは描けますか?
「大きさ」を知りたいなら、視覚的な情報が得られれば効率よく答えが得られそうですよね。
何も手が打てない!というときは、落書き程度のグラフを描いてみましょう。
解法のきっかけが得られることが多いですよ。

Lukia
上のグラフが、\( \ y=\log_{2}x \ \)のグラフです。
まどろっこしい書き換えをしてみますが、
\( \ \log_{2}2=\log_{2}2^1=1 \ \)でした。
つまり、\( \ 10 \ \)とは、\( \ 2 \ \)を底とする指数で表現したとき、\( \ 2^n \ \)と\( \ 2^{n+1}\quad \left( nは自然数\right) \ \)の間に存在するとして、その自然数\( \ n \ \)はいったいいくつなのか?を求めればいいことになります。
まどろっこしい書き換えをしてみますが、
\( \ \log_{2}2=\log_{2}2^1=1 \ \)でした。
つまり、\( \ 10 \ \)とは、\( \ 2 \ \)を底とする指数で表現したとき、\( \ 2^n \ \)と\( \ 2^{n+1}\quad \left( nは自然数\right) \ \)の間に存在するとして、その自然数\( \ n \ \)はいったいいくつなのか?を求めればいいことになります。

Lukia
与えられた対数に対して、底の変換公式を用いたことにより、不等式がすべて分数の形で表されました。
ここからは、ことわりを入れて、逆数の形に直し、(整数のような状態になりますね)
自然数\( \ n \ \)を求めてみます。
ここからは、ことわりを入れて、逆数の形に直し、(整数のような状態になりますね)
自然数\( \ n \ \)を求めてみます。
$$\begin{align}&各辺の逆数をとると \\\\ n \lt &\log_{2}10 \lt n+1\quad と表せる. \\\\ さらに&\log_{2}10\quad を \ 2を底とする指数で考える.\\\\ 2^3 \lt &10 \lt 2^4\quad より\\\\ &求める自然数 \ n \ は\quad 3 \end{align}$$
分数の値の大小をイメージするなら「分母」を意識しよう

Lukia
分数のときは、左端の辺の分母は\( \ n+1 \ \)でしたが、逆数(分数から整数の形に変える)だと、\( \ n+1 \ \)は右端の辺に移動していますね。
分数のときは、分母の数が大きくなればなるほど、その値は小さくなるというのを再確認しておくとよいと思います。
感覚的にわかってもらうなら、ホールのケーキを何人で分けるか。というたとえがいいかも。
誕生日ケーキだとすると、祝ってくれる人の数が多いほうがにぎやかで嬉しいけれど、
一人あたりの食べられるケーキのピースの大きさは小さくなっていきます。
分数のときは、分母の数が大きくなればなるほど、その値は小さくなるというのを再確認しておくとよいと思います。
感覚的にわかってもらうなら、ホールのケーキを何人で分けるか。というたとえがいいかも。
誕生日ケーキだとすると、祝ってくれる人の数が多いほうがにぎやかで嬉しいけれど、
一人あたりの食べられるケーキのピースの大きさは小さくなっていきます。

Lukia
人気アイドルが1万人のファンに誕生日を祝われ、
まぁまぁ見栄えのする直径50センチぐらいのホールケーキを分けて食べるとしたら。
ミキサーにかけないと分けられませんし、(もはや、ケーキの面影はない)
しずくレベルの元ケーキが口に入ればいいほうでしょう。「あー、誕生日イベントでケーキを分けるのはナシだな。」と思いますね。
(数学をするようになって、最近はもっぱらこういうくだらない妄想をしています。)
まぁまぁ見栄えのする直径50センチぐらいのホールケーキを分けて食べるとしたら。
ミキサーにかけないと分けられませんし、(もはや、ケーキの面影はない)
しずくレベルの元ケーキが口に入ればいいほうでしょう。「あー、誕生日イベントでケーキを分けるのはナシだな。」と思いますね。
(数学をするようになって、最近はもっぱらこういうくだらない妄想をしています。)
こたえ
$$n=3$$
[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません