高校数学の「三角不等式（コサインに合成バージョン）」に関する問題を解いてみる。（Yahoo!知恵袋より）

2018年10月13日2023年1月15日三角関数実用数学技能検定（数学検定 数検),数検2級

[mathjax]

左辺をコサインに合成する。

Lukia

左辺を
\(-\cos \theta+\sqrt{3}\sin \theta\)　と書き換えます。
合成することによってなす角は、原点から\(\color{red}{x軸方向に-1}\)、
\(\color{blue}{y軸方向に+\sqrt{3}}\)進んだ位置と原点を結んだ線分と、\(x軸\)によってあらわされます。
図に表すと、以下のようになります。

Lukia

線分の長さは、\(\sqrt{\color{red}{\left( -1\right)^2}+\color{blue}{\left( \sqrt{3}\right)^2}}=2\)　となりますね。

$$\begin{align}-\cos \theta+\sqrt{3}\sin \theta=&2\cos \left( \theta\color{red}{-}{\frac{ 2 }{ 3 }}\pi\right) \end{align}$$

Lukia

コサインに合成するときは、\(\theta\)と新たになす角をマイナスでつなぎます。
理由はあるんでしょうが、そんなことうじゃうじゃ考えるよりは、覚えて使えるようになったほうがいいので、
そういうもんだと覚えてください。

θの範囲をそろえる。

$$\begin{align}0 \leq &\theta \leq \pi \\\\ -{\frac{ 2 }{ 3 }}\pi \leq &\theta-{\frac{ 2 }{ 3 }}\pi \leq\pi-{\frac{ 2 }{ 3 }}\pi
\\\\ -{\frac{ 2 }{ 3 }}\pi \leq &\theta-{\frac{ 2 }{ 3 }}\pi \leq \frac{ \pi }{ 3 } \end{align}$$

Lukia

半径1の単位円で表すと、以下の図の水色に塗られた部分にあたります。

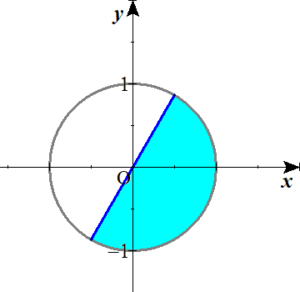
$$-\frac{1}{2} \leq \cos \left( \theta-{\frac{ 2 }{ 3 }}\pi\right) \leq 1$$

不等式を解く。

$$\begin{align}-\cos \theta+\sqrt{3}\sin \theta \lt &\sqrt{3} \\\\ 2\cos \left( \theta-{\frac{ 2 }{ 3 }}\pi\right) \lt &\sqrt{3}
\\\\ \cos \left( \theta-{\frac{ 2 }{ 3 }}\pi\right) \lt &\frac{\sqrt{3}}{2} \end{align}$$

Lukia

一般的に、
\(\cos \theta\)は、単位円において、
\(\theta=2n\pi\) (以下、\(n\)は\(0\)以上の整数）のとき、最大値\(1\)をとり、
\(\theta=\left( 2n+1\right)\pi\)のとき、最小値\(-1\)を取ります。

Lukia

いま、問題は、
\(\cos \left( \theta-{\frac{ 2 }{ 3 }}\pi\right)\)の値が\(\frac{\sqrt{3}}{2}\)よりも小さい範囲はどこか？
と問うているので、
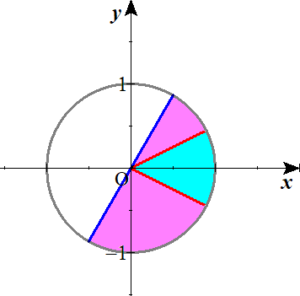
さきほど、水色に塗られた部分にその条件を重ね合わせると、
以下の図のピンクで塗りつぶされた部分が相当するとわかります。

Lukia

図を参考にしながら、範囲を書き起こします。

$$\begin{align}-{\frac{ 2 }{ 3 }}\pi \leq &\theta-{\frac{ 2 }{ 3 }}\pi \lt -\frac{ \pi }{ 6 } \\\\すなわち、0 \leq &\theta \lt \frac{ \pi }{ 2 } \cdots　①\ & \end{align}$$
$$\begin{align}\frac{ \pi }{ 6 } \lt &\theta-{\frac{ 2 }{ 3 }}\pi \leq \frac{ \pi }{ 3 } \\\\すなわち、 {\frac{ 5 }{ 6 }}\pi \lt &\theta \leq \pi \cdots　② \end{align}$$

こたえ

$$0 \leq \theta \lt \frac{ \pi }{ 2 }$$
$$ {\frac{ 5 }{ 6 }}\pi \lt \theta \leq \pi$$

センター試験では、コサインに合成するバージョンが出たこともあるので。

三角関数の合成は、サインに合成するパターンが多いのですが、
センター試験は、しれ～っと落とし穴（？）をしかけるのが大好きです。
ですから、ときどき、コサインに合成する誘導がなされていることもあります。

まずは、サインで合成するパターンを体得したら、同じ問題でコサインに合成する練習もしてみましょう。
答えが確実にわかっているのですから、安心して練習できますからね。

高校数学の「三角不等式（サインに合成バージョン）」に関する問題を解いてみる。（Ya

問題 \(0 \leq \theta \leq \pi\)のとき、 不等式 \(\sqrt{3}\sin \theta-\cos \theta \lt \sqrt{3}\) ...

 https://makelemonadejp.com/yc-18

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。