高校数学の「三角不等式（サインに合成バージョン）」に関する問題を解いてみる。（Yahoo!知恵袋より）

2018年10月12日2023年1月15日三角関数実用数学技能検定（数学検定 数検),数検2級

[mathjax]

左辺を合成する。

Lukia

三角関数の合成を行います。
与式を\(\sin \left( \theta+\alpha\right)\)　のような形にしてみます。
\(\sqrt{3}\sin \theta-\cos \theta\)は、
\(\color{red}{+\sqrt{3}}\sin \theta\color{blue}{-}\cos \theta\) と考えます。
さらに\(\sin \theta\)を「\(\color{red}{x軸方向に}\)」とし、
\(\cos \theta\)を「\(\color{blue}{y軸方向に}\)」と読み替えます。

Lukia

つまり、\(\sqrt{3}\sin \theta-\cos \theta\)を合成することでなす角は、
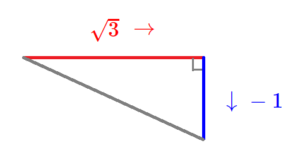
原点から\(\color{red}{x軸方向に+\sqrt{3}}\)進み、\(\color{blue}{y軸方向に-1}\)進んだ点と原点を結んだ線分と\(x\)軸とのなす角に相当するのです。
上の図の灰色の線と赤い線（\(x\)軸上にありますから）のなす角は、\(-\frac{ \pi }{ 6 }\)
灰色の線分の長さは、\(\sqrt{\color{red}{\left( \sqrt{3}\right)^2+\color{blue}{\left( -1\right)^2}}}=2\) とわかります。

$$\begin{align}\sqrt{3}\sin \theta-\cos \theta=&\sqrt{\left( \sqrt{3}\right)^2+\left( -1\right)^2}\sin \left( \theta-\frac{ \pi }{ 6 }\right) \\\\ =&2\sin \left( \theta-\frac{ \pi }{ 6 }\right) \end{align}$$

範囲をそろえる。

Lukia

式を合成することによって、
\(\theta\)ではなく、\(\theta-\frac{ \pi }{ 6 }\)で考える必要が出てきました。

$$\begin{align}0 \leq &\theta \leq \pi \\\\ -\frac{ \pi }{ 6 } \leq &\theta-\frac{ \pi }{ 6 } \leq \pi-\frac{ \pi }{ 6 } \\\\ -\frac{ \pi }{ 6 } \leq &\theta-\frac{ \pi }{ 6 } \leq {\frac{ 5 }{ 6 }}\pi \end{align}$$

Lukia

半径1の単位円で考えると、
以下の図の水色に塗られた部分にあたります。

不等式を解く。

$$\begin{align}\sqrt{3}\sin \theta-\cos \theta \lt &\sqrt{3} \\\\ 2\sin \left( \theta-\frac{ \pi }{ 6 }\right) \lt &\sqrt{3}
\\\\ \sin \left( \theta-\frac{ \pi }{ 6 }\right) \lt &\frac{\sqrt{3}}{2} \end{align}$$

Lukia

\(0 \leq x \lt 2\pi\)　において、
\(\sin x=\frac{\sqrt{3}}{2}\)を満たす\(x\)は、\(x=\frac{ \pi }{ 3 } , x={\frac{ 2 }{ 3 }}\pi\) ですね。
つまり、\(\theta-\frac{ \pi }{ 6 }\)は、以下の図のピンクで塗りつぶされた部分に存在する必要があります。

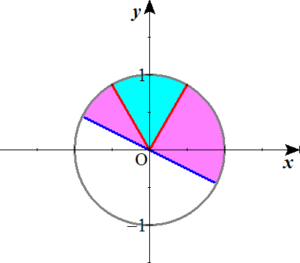
$$\begin{align}-\frac{ \pi }{ 6 } \leq &\theta-\frac{ \pi }{ 6 } \lt \frac{ \pi }{ 3 } \\\\ \ 0 \leq &\theta \lt \frac{ \pi }{ 2 } \cdots　①\end{align}$$

$$\begin{align}{\frac{ 2 }{ 3 }}\pi \lt &\theta-\frac{ \pi }{ 6 } \leq {\frac{ 5 }{ 6 }}\pi \\\\ \ {\frac{ 5 }{ 6 }}\pi \lt &\theta \leq \pi \cdots　②\end{align}$$

こたえ

$$\begin{align}0 \leq &\theta \lt \frac{ \pi }{ 2 } \\\\ {\frac{ 5 }{ 6 }}\pi \lt &\theta \leq \pi \end{align}$$

コサインに合成バージョンも書いてみます。

センター試験では、コサインに合成するよう誘導された問題が出たことがあります。
サインに合成できるようになったら、少しポイントをおさえるだけで、
コサインに合成することもできるようになります。
まったく同じ問題を解いていますので、二つの記事を比べて、合成するパターンを体得してください。

高校数学の「三角不等式（コサインに合成バージョン）」に関する問題を解いてみる。（

問題 \(0 \leq \theta \leq \pi\)のとき、 不等式 \(\sqrt{3}\sin \theta-\cos \theta \lt \sqrt{3}\) ...

 https://makelemonadejp.com/yc-19

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。