高校数学の「2つのベクトルを用いて新たなベクトルを表現する」に関する問題を解いてみる。（Yahoo!知恵袋より）

2019年10月28日2023年1月13日ベクトル実用数学技能検定（数学検定数検),数検2級,数検準1級

読了時間: 約4分34秒

[mathjax]

問題

三角形$ \ \mathrm{OAB} \ $において、$ \ \overrightarrow{\mathrm{OA}}=\vec{a} \ $,$ \ \overrightarrow{\mathrm{OB}}=\vec{b} \ $とし,
$ \ \vert \vec{a} \vert =3 \ , \ \vert \vec{b} \vert=2 \ , \ \angle \mathrm{AOB}=60^{\circ} $とする。
ここで、$ \ \angle \mathrm{AOC}=90^{\circ} \ $となるように、直線上に点$ \ \mathrm{C} \ $をとる。
このとき、$ \ \overrightarrow{\mathrm{OC}} \ $を$ \ \vec{a} \ , \ \vec{b} \ $を用いて表せ。

わかっていることを数学語で表現しよう。

Lukia

直線$ \ \mathrm{AB} \ $上に点$ \ \mathrm{C} \ $が存在する。ということですから、以下のような表現ができます。

$$\overrightarrow{\mathrm{AC}}=k\overrightarrow{\mathrm{AB}}\quad \left( kは実数\right)\quad \cdots①$$

Lukia

今回問題を解くにあたって、定数$ \ k \ $を置きました。数学に長ったらしい日本語を書くのは、めんどくさいでしょうが、自分が勝手に置いたものですから、必ずことわりが必要です。
また、数には実数と虚数（$ \ i \ $で表現されるもの）が存在しますので、なんらかの大きさが存在する実数の世界で考えますよ。と宣言しておきましょう。

$$\begin{align}また、&\angle \mathrm{AOC}=90^{\circ} \ より \\\\ &\overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OC}}=0\quad \cdots② \end{align}$$

$$\begin{align}\frac{\vec{a}\cdot \vec{b}}{\vert \vec{a} \vert\vert \vec{b} \vert}=&\cos 60^{\circ} \\\\ \frac{\vec{a}\cdot \vec{b}}{3\cdot 2}=&\frac{1}{2}\\\\ \\\\ \vec{a}\cdot \vec{b}=&3\quad \cdots③ \end{align}$$

①に集約させます。

①を変形する。
$$\begin{align}\overrightarrow{\mathrm{AC}}=&k\overrightarrow{\mathrm{AB}} \\\\ \vec{c}-\vec{a}=&k\left( \vec{b}-\vec{a}\right)\quad \cdots④\end{align}$$
$$\begin{align}辺々 \ \vec{a}& \ をかける. \\\\ \vec{a}\cdot \vec{c}-\vert \vec{a} \vert^2=&k\left( \vec{a}\cdot \vec{b}-\vert \vec{a} \vert^2\right) \\\\ -9=&-6k\\\\ k=&\frac{3}{2} \end{align}$$
④に代入して整理する。
$$\begin{align}\vec{c}=&\vec{a}+\frac{3}{2}\left( \vec{b}-\vec{a}\right) \\\\ =&\frac{1}{2}\left( 2\vec{a}+3\vec{b}-3\vec{a}\right) \\\\ \vec{c}=&-\frac{1}{2}\left( \vec{a}-3\vec{b}\right) \end{align}$$

点Cの位置を図形で確認する。

Lukia

図形描画ソフトで描こうと四苦八苦したものの、時間ばっかりかかってうまくいかなかったので、コンパスとものさしを使って手描きしてみました。

Lukia

式の変形や計算を経て、
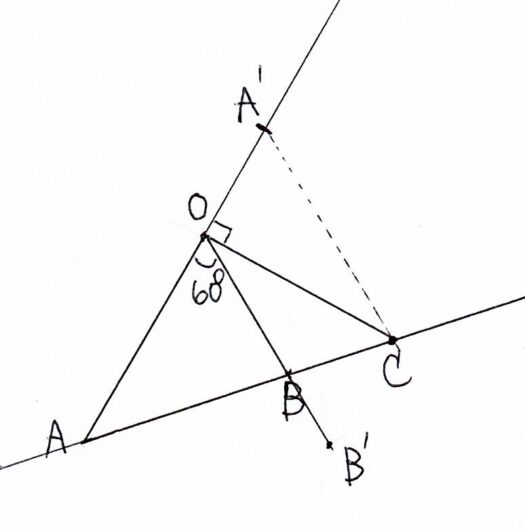
$ \ \vec{a}=-\frac{1}{2}\vec{a}+\frac{3}{2}\vec{b} \ $と表されることがわかりました。
まず、$ \ \overrightarrow{\mathrm{OA}} \ $とは逆向きで、長さ1.5の位置に点$ \ \mathrm{A’} \ $を打ちます。
同様に$ \ \overrightarrow{\mathrm{OB}} \ $と同じ向きで、長さ3の位置に点$ \ \mathrm{B’} \ $を打ちます。
すなわち、$ \ \overrightarrow{\mathrm{OC}} \ $は、$ \ \overrightarrow{\mathrm{OA’}} \ $と$ \ \overrightarrow{\mathrm{OB’}} \ $が合成したものといえます。

Lukia

点$ \ \mathrm{C} \ $は直線$ \ \mathrm{AB} \ $上にありますし、$ \ \angle \mathrm{AOC}=90^{\circ} \ $となっていますね。

目分量の精度をあげておこう。

わざわざ、手描きで図を描いたのは、解答の際に描いた図があまりにいい加減すぎて、
答えが本当に正しいのかどうか、判断できなかったからです。

大学入試センター試験では、コンパスはもちろんものさしも持ち込み不可なので、短時間でできるだけ正確な図を描ける力が必要となります。

フリーハンドでまっすぐな線が引ける、あるいはきれいな円が描けるというのは、高校数学においては、なかなかのアドバンテージになります。
しかし、この能力は一朝一夕で身につくようなものではありません。

勉強しなきゃいけないけど、何も手につかない。というようなときは、まずは、まっすぐな線を引くとか、真円に近づけるなどの練習をしてみましょう。
あとは、なるべく正確な目盛りの感覚を身に着けるというのも必要だと思います。
今回の問題ですと、長さ2と3の線分、60°という角度が出てきました。
私は、60°をできるだけ正確に描かなかったため、点Cの位置が直線AB上になく、

Lukia

本当に合ってるの？（汗）

と不安になってしまいました。

長さ3の正三角形（に近いもの）を描いておいて、ある辺上に長さ2になるように点を打てば、結構簡単に三角形OABが描けたはずですね。

目分量がものさしの目盛り並の精度になれば、こういう幾何系の問題はおおいに助けられます。
気楽にたくさん練習して、精度を上げておきましょう。