高校数学の「絶対値を含む関数の最小値」に関する問題を解いてみる。（Yahoo!知恵袋より）
[mathjax]
甘いものがあるところ、ヤツは現れる。（汗）
Lukia
今日は、平日の唯一の休み。でろ〜んとするぞぉ♪
そうだ！今日のおやつは、水ようかんにしよう。
いっぱい記事を書いて、頭クラクラさせて、甘い水ようかんを食べるんだ〜♪むふふ・・・。
ドシン！・・・ドシン！・・・
グラスのアイスコーヒーに丸い水紋が浮かびます。
Lukia
火事、親父？
私の場合、怖いのは親父ってよりは、ディノさんだな〜。にゃはは〜♪
ディノ
Lukia
き、今日は、絶対値の問題、ありませんよ？
私、別の記事書くつもりなんですからッ！（汗）
ディノ
オレは、水ようかん食べに来ただけだし。
Lukia
ディノ
Lukia
水ようかんだけは、タダではあげられません！
母のお腹の中にいるときから、あんこ好きだった私。
母は、私がお腹にいるとき、やたらとあんパンやら、あんドーナツやらを食べていたそうです。
おそらく、母が何の気なしに食べたあんパンを、胎内の私が気に入ったんだと思います。
その後もあんこ好きは続き、
幼い頃、祖父母の家に届くお中元の水ようかんは、ほとんど私のお腹に入っていったものです。(笑)
いつもは、ディノさんにスイーツを譲ってあげていますが、水ようかんは無理ッ！
ディノ
くれたら、おとなしくしとくからよぉ〜。
Lukia
おとなしい肉食恐竜なんて、ただおもしろいだけでしょ！
ディノ
オレも食べたいよ〜〜〜〜！
頼むよ〜〜〜！
たしかに。水ようかんの魅力は抑えがたいよね。
Lukia
じゃ、今から出す問題を、ディノさんだけで解けたら、一個あげます。
一個だけですよ！？
ディノ
解いたらくれるんだな？絶対だな？
Lukia
解けて、水ようかんあげたら・・・
ディノ
おとなしくしてる！
邪魔しない！
Lukia
というわけで、ディノさんに、見た目に難しそうな問題を出してみることにしました。
ディノさん 自力で解く。
ディノ
絶対値記号が2つあるパターンはこれまでも見てきたけど、4つは初めてだ。
アイツ、よっぽど水ようかん取られたくないんだな。
ディノ
まずはそれぞれの絶対値記号に挟まれた式ごとに考えていけばいい。
V字型のグラフと表でまとめてみるか。
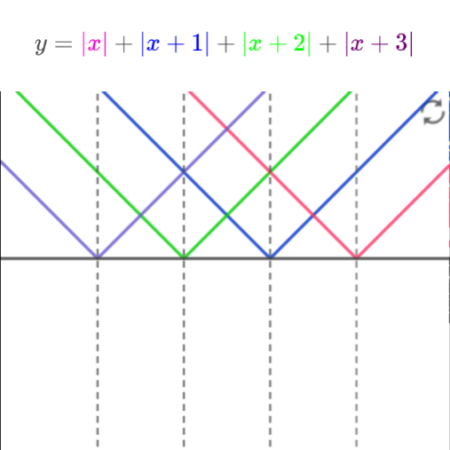
ディノ
・・・すげぇ顔してこっち見るなよ！（汗）
Lukia
ほかにもやることあるんですから。
ディノ
5つの範囲に絶対値の記号をはずして式を書き込んでみるか。
すると、こうなるな。
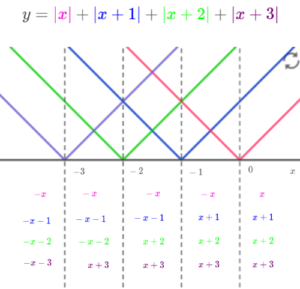
ディノ
すると、各範囲でまとめた式がこうなる。
$$\begin{align}y=&\vert x \vert+\vert x+1 \vert+\vert x+2 \vert+\vert x+3 \vert\ \\\\ y=&-4x-6\quad \left( x \lt -3\quad のとき\right) \\\\ y=&-2x\quad \left( -3 \leq x \lt -2\quad のとき\right) \\\\ y=&4\quad \left( -2 \leq x \lt -1\quad のとき\right) \\\\ y=&2x+6\quad \left( -1 \leq x \lt 0\quad のとき\right) \\\\ y=&4x+6\quad \left( 0 \leq x\quad のとき\right) \end{align}$$
ディノ
ディノ
お〜い、水ようかん冷やしてあるか〜？
Lukia
ディノ
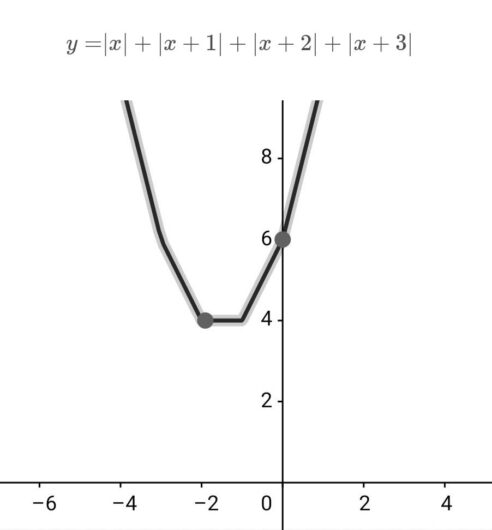
最小値は、グラフを読み取るだけだな。
\( \ 4 \ \)が最小値だな。
Lukia
ディノ
\( \ -2 \leq x \leq -1 \ \)となる。
Lukia
ディノ
Lukia
ディノ
Lukia
ディノ
優しいヤツだと思ってたんだよ〜〜〜、オレは〜〜〜♪
というわけで、ディノさんと一緒に水ようかんの甘さにとろけたのでした。
この後、邪魔しちゃ悪いからな。と帰っていくあたり、
にくめないんだよね、ディノさん。(笑)
こたえ
$$最小値：4\quad \quad -2 \leq x \leq -1$$
共有:
プロフィール
