高校数学の「三角関数の最大値・最小値」に関する問題を解いてみる。（Yahoo!知恵袋より）

2018年10月11日2023年1月15日三角関数実用数学技能検定（数学検定 数検),数検2級

[mathjax]

θの範囲を変形する。

$$\begin{align}0 \leq &\theta \leq \pi \\\\0\color{blue}{-\frac{ \pi }{ 6 }} \leq &\theta\color{blue}{-\frac{ \pi }{ 6 }} \leq \pi \color{blue}{-\frac{ \pi }{ 6 }} \\\\ -\frac{ \pi }{ 6 } \leq &\theta-\frac{ \pi }{ 6 } \leq {\frac{ 5 }{ 6 }}\pi \end{align}$$

Lukia

半径1の単位円で表すと、\(\theta-\frac{ \pi }{ 6 }\)の範囲は、
水色に塗られた部分となります。

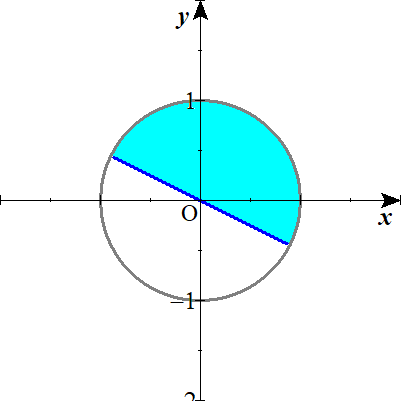
サインの最大値・最小値を求める。

Lukia

以前別のページで、「\(\sin\)(サイン）は\(y\)（ワイ）」という恩師直伝のダジャレについて書いたと思いますが、今回もそれが使えます。
単位円の水色に塗られた部分において、最も高い位置と最も低い位置はどこか。と聞かれているのにすぎません。

れもん

ということは、\(y=1\)になるときが最も高く、
\(y=-\frac{1}{2}\)になるときが最も低いことになりますね。

Lukia

そうです。図では以下のようになりますね。

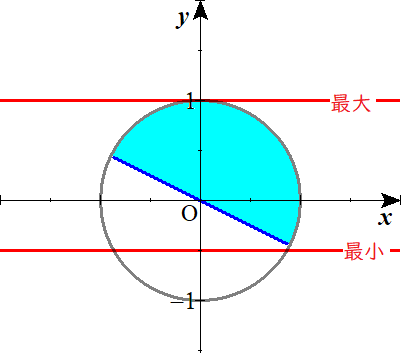
Lukia

三角関数は、単位円を描くことでイメージ化しやすくなるので、
当然、解きやすくなります。

$$-\frac{1}{2} \leq \sin \left( \theta-\frac{ \pi }{ 6 }\right) \leq 1$$
ゆえに、
$$\begin{align}最大値： 1　　&\theta-\frac{ \pi }{ 6 }=\frac{ \pi }{ 2 } \\\\ すなわち、&\theta={\frac{ 2 }{ 3 }}\pi のとき
\\\\最小値： -\frac{1}{2}　　&\theta-\frac{ \pi }{ 6 }=-\frac{ \pi }{ 6 } \\\\ すなわち、&\theta=0 のとき \end{align}$$

こたえ

$$最大値： 1　　\theta={\frac{ 2 }{ 3 }}\pi のとき$$
$$最小値： -\frac{1}{2}　　\theta=0 のとき$$

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。