高校数学の「中央値の場合分け」に関する問題を解いてみる。（Yahoo!知恵袋より）

2019年4月17日2023年1月14日データの分析実用数学技能検定（数学検定 数検),数検準2級

[mathjax]

定数aの入る位置を考える。

a を除く7つのデータを左から小さい順に並べると以下の通り.
$$27 \ , \ 30 \ , \ 31 \ , \ 35 \ , \ 37 \ , \ 38 \ , \ 41$$
$$また,\quad {8} \equiv {0} \pmod {4}\quad より$$
中央値は左から4番目と5番目のデータの平均であり,
a が入るのは①～⑧の8ヶ所が考えられる。

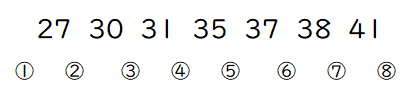
a を①から⑧の位置に入れて、8つのデータを左から小さい順に並べたものが以下の表である。

$$\begin{align}左から&小さい順に並べて \ 4番目の数を\quad \alpha \\\\左から&小さい順に並べて \ 5番目の数を\quad \beta\quad とする.\\\\ 中央値は&\quad \frac{\alpha+\beta}{2}\quad で求められ, \\\\ 大きく&4つの場合が考えられる.\\\\ 1：\quad &\frac{\alpha+\beta}{2}=\frac{31+35}{2}=33\quad ①～③\\\\ 2：\quad &\frac{\alpha+\beta}{2}=\frac{a+35}{2}\quad ④\\\\ 3：\quad &\frac{\alpha+\beta}{2}=\frac{35+a}{2}\quad ⑤\\\\ 4：\quad &\frac{\alpha+\beta}{2}=\frac{35+37}{2}=36\quad ⑥～⑧\end{align}$$

以下、aが④の位置にある場合と、aが⑤の位置にある場合の中央値を求める.

aが④の位置にある場合の中央値を求める。

$$\begin{align}31 \lt a \leq 35&\quad のとき, \\\\ a=&32 \ , \ 33 \ , \ 34 \ , \ 35\quad が考えられる. \\\\ \frac{a+35}{2}=&\frac{\color{#0004fc}{32}+35}{2} \ , \\\\ \frac{a+35}{2}=&\frac{\color{#0004fc}{33}+35}{2} \ , \\\\ \frac{a+35}{2}=&\frac{\color{#0004fc}{34}+35}{2} \ , \\\\ \frac{a+35}{2}=&\frac{\color{#0004fc}{35}+35}{2}\ \\\\ 中央値は&33.5 \ , \ 34 \ , \ 34.5 \ , \ 35\quad の4通り. \end{align}$$

aが⑤の位置にある場合の中央値を求める。

$$\begin{align}35 \lt a \leq 37&\quad のとき, \\\\ a=&36 \ , \ 37\quad が考えられる. \\\\ \frac{35+a}{2}=&\frac{35+\color{#0004fc}{36}}{2} \ , \\\\ \frac{35+a}{2}=&\frac{35+\color{#0004fc}{37}}{2}\ \\\\ 中央値は&35.5 \ , \ 36\quad の2通り. \end{align}$$
以上より考えられる中央値は,
$$33 \ , \ 33.5 \ , \ 34 \ , \ 34.5 \ , \ 35 \ , \ 35.5 \ , \ 36$$
の7通り.

こたえ

7通り

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。