高校数学の絶対値の問題は、グラフでイメージしよう。(その6)

読了時間: 約4分51秒
[mathjax]
自宅のパソコンでブログ記事を書いていたはずが、
突然不思議な世界に迷い込み、
高校生?恐竜、ディノさんと出会ってしまった私。
ディノさんは、絶対値の問題の解き方を教えてくれたら、ひらけた場所までの案内をしてくれると言いますが・・・
さて、今日の問題の「解法」で、ディノさんは私を「解放」してくれるのでしょうか。
![]()

ディノ
ぷは~、うまかったなぁ。パフェ。

Lukia
ディノさん、お腹がいっぱいです。。。

ディノ
でも、なんだかんだ言って、
抹茶パフェ、食ってたじゃねぇかよ。
うまかったんだろ?
抹茶パフェ、食ってたじゃねぇかよ。
うまかったんだろ?


Lukia
たしかに。
でも、不思議なことに、問題解いてお店に向かったら、あれほど胃もたれしてたのに、
お腹空いてましたね。
なんですか、ここはそういう設定ですか?
でも、不思議なことに、問題解いてお店に向かったら、あれほど胃もたれしてたのに、
お腹空いてましたね。
なんですか、ここはそういう設定ですか?

ディノ
んまぁ、よくわかんないが、そういう設定だ。
というわけで、今回も問題解けば、腹が減って、次のうまいもん食いに行けるってことだ。
というわけで、今回も問題解けば、腹が減って、次のうまいもん食いに行けるってことだ。

Lukia
ふぇいふぇい。
(食べ物でしばらく釣る気だな・・・)
(食べ物でしばらく釣る気だな・・・)
問題
$$\Large \color{blue}{\vert x-2 \vert}+\color{red}{\vert \frac{x}{3}-2 \vert}=2$$
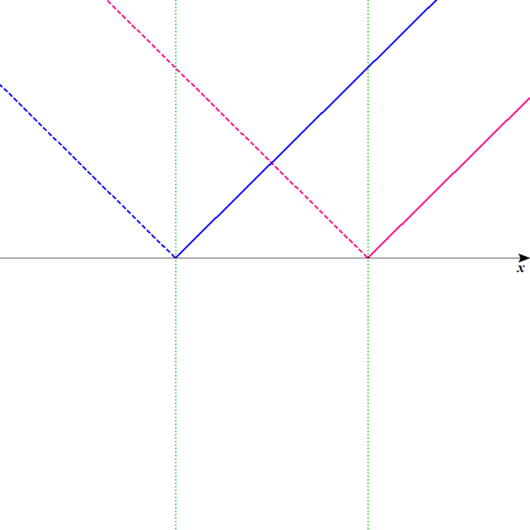
簡単な図を描こう。

Lukia
さて、今回も以下のような図を使います。
計算のスペースが必要になるので、グラフの下はあけておいてくださいね。
計算のスペースが必要になるので、グラフの下はあけておいてくださいね。
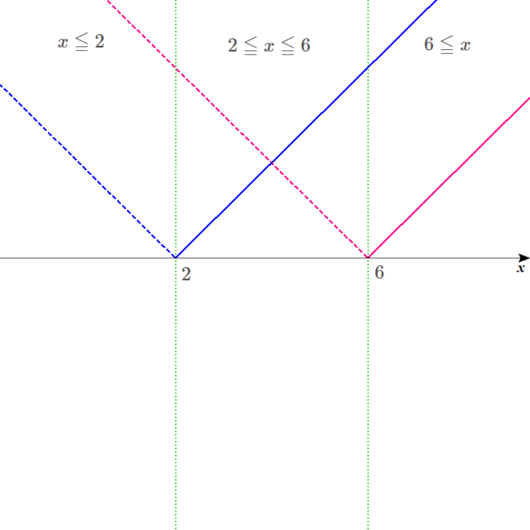
範囲を設定しよう。

Lukia
ディノさん、もう慣れてきたと思いますので、
二つのV字グラフが、\(x\)軸と交わるときの\(x\)の値を求めてください。
二つのV字グラフが、\(x\)軸と交わるときの\(x\)の値を求めてください。

ディノ
任せとけ!
まず、\(\color{blue}{\vert x-2 \vert=0}\)となるのは、
\(x=\color{blue}{2}\)のときで、
まず、\(\color{blue}{\vert x-2 \vert=0}\)となるのは、
\(x=\color{blue}{2}\)のときで、

ディノ
\(\color{red}{\vert \frac{x}{3}-2 \vert=0}\)となるのは、
\(x=\color{red}{6}\)のときだな。
\(x=\color{red}{6}\)のときだな。

Lukia
そうですね。
というわけで、図に範囲などを書き込んでおきます。
以下のような図になりますね。
というわけで、図に範囲などを書き込んでおきます。
以下のような図になりますね。
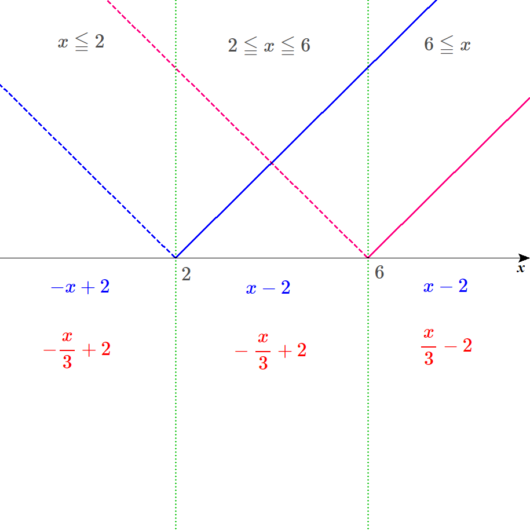
範囲ごとに式を書き込んでいく。

ディノ
次の手順は、覚えたぞ。
範囲ごとに式を書き込んでいくんだ。
まず、青いグラフから片付けるとして・・・
\(\color{blue}{y=\vert x-2 \vert}\)は、
\(y=\color{blue}{-x+2}\) \(\left( \color{blue}{x \leq 2} のとき\right)\)
\(y=\color{blue}{x-2}\) \(\left( \color{blue}{2 \leq x} のとき\right)\) だから、
それらを範囲に合うように書き込めばいいんだったよな。
範囲ごとに式を書き込んでいくんだ。
まず、青いグラフから片付けるとして・・・
\(\color{blue}{y=\vert x-2 \vert}\)は、
\(y=\color{blue}{-x+2}\) \(\left( \color{blue}{x \leq 2} のとき\right)\)
\(y=\color{blue}{x-2}\) \(\left( \color{blue}{2 \leq x} のとき\right)\) だから、
それらを範囲に合うように書き込めばいいんだったよな。

Lukia
はい。そして・・・

ディノ
オマエ、腹いっぱいでしゃべれねぇだろうから、
オレがやってやる。
赤いグラフも同じようにやればいいんだから、
\(\color{red}{y=\vert \frac{x}{3}-2 \vert}\)は、
\(y=\color{red}{-\frac{x}{3}+2}\) \(\left( \color{red}{x \leq 6} のとき\right)\)
\(y=\color{red}{\frac{x}{3}-2}\) \(\left( \color{red}{6 \leq x} のとき\right)\) となって、
やっぱりこれも、範囲に合うように書き込むんだったよな。
どうだ、できたぞ。
オレがやってやる。
赤いグラフも同じようにやればいいんだから、
\(\color{red}{y=\vert \frac{x}{3}-2 \vert}\)は、
\(y=\color{red}{-\frac{x}{3}+2}\) \(\left( \color{red}{x \leq 6} のとき\right)\)
\(y=\color{red}{\frac{x}{3}-2}\) \(\left( \color{red}{6 \leq x} のとき\right)\) となって、
やっぱりこれも、範囲に合うように書き込むんだったよな。
どうだ、できたぞ。

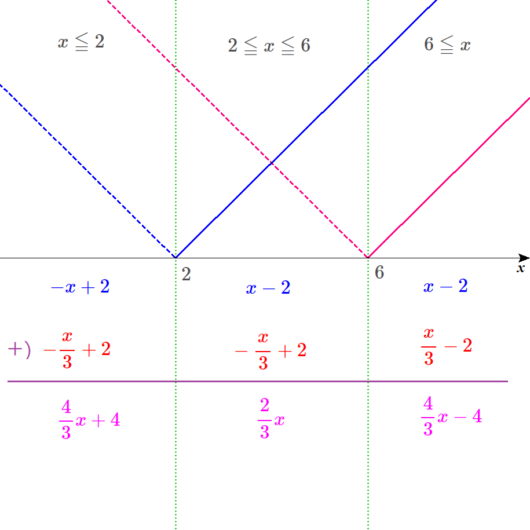
Lukia
ご配慮、いたみいります。
(ああ、こういうパターン以前にもありましたねぇ・・・。
ももちゃん、どうしてるかな・・・)
(ああ、こういうパターン以前にもありましたねぇ・・・。
ももちゃん、どうしてるかな・・・)
筆算する。

Lukia
ディノさん、順調に手順を踏んでますね。
というわけで、次にやるのは・・・
というわけで、次にやるのは・・・

ディノ
筆算だ!
二つの絶対値は、+(プラス)でつながれているから、
たし算の筆算をすればいいんだったよな。
・・・
できたぞ!
二つの絶対値は、+(プラス)でつながれているから、
たし算の筆算をすればいいんだったよな。
・・・
できたぞ!

Lukia
なるほど。
左が、\(\frac{4}{3}x+4\)
真ん中が、\(\frac{2}{3}x\)
右が \(\frac{4}{3}x-4\)になるんですね。
左が、\(\frac{4}{3}x+4\)
真ん中が、\(\frac{2}{3}x\)
右が \(\frac{4}{3}x-4\)になるんですね。
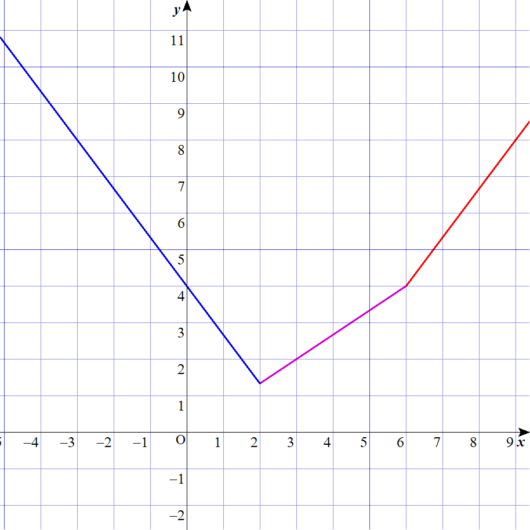
グラフを描くとこうなる。

Lukia
ちなみに、ディノさんが筆算で導き出した三つの式をグラフにすると、
以下のようになります。
以下のようになります。
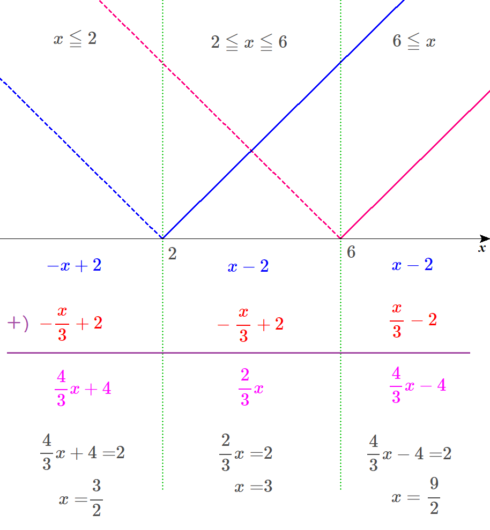
方程式を解く。

Lukia
さて、ここまでは、左辺の式を変形してきました。
いよいよ、=2 をつけて、方程式を解いてみましょう。
いよいよ、=2 をつけて、方程式を解いてみましょう。

ディノ
じゃ、左の範囲の方程式をオレが解く。
\(\frac{4}{3}x+4=2\) を解くと
\(x=\frac{3}{2}\) とわかる。
\(\frac{4}{3}x+4=2\) を解くと
\(x=\frac{3}{2}\) とわかる。

Lukia
では、真ん中の範囲の方程式は、私が解きましょう。
\(\frac{2}{3}x=2\) を解いて、
\(x=3\) が答えとなりますね。
\(\frac{2}{3}x=2\) を解いて、
\(x=3\) が答えとなりますね。

ディノ
じゃ、右の範囲の方程式は、オレだな。
\(\frac{4}{3}x-4=2\) を解けばいいんだから、
、\(x=\frac{9}{2}\) が答えだ。
\(\frac{4}{3}x-4=2\) を解けばいいんだから、
、\(x=\frac{9}{2}\) が答えだ。
範囲を比較して答えを出す。

Lukia
三つの範囲の方程式の解を、実際に\(x\)軸上に置いてみましょう。
左の範囲の解は、青い四角で囲み、\(x\)軸には、青い矢印で、だいたいの位置を示します。
真ん中の範囲の解は、紫の四角で囲み、\(x\)軸には、紫の矢印で、だいたいの位置を示します。
右の範囲の解は、赤い四角で囲み、\(x\)軸には、赤い矢印で、だいたいの位置を示します。
すると、以下のようになるのですが、ディノさん、いかがですか?
左の範囲の解は、青い四角で囲み、\(x\)軸には、青い矢印で、だいたいの位置を示します。
真ん中の範囲の解は、紫の四角で囲み、\(x\)軸には、紫の矢印で、だいたいの位置を示します。
右の範囲の解は、赤い四角で囲み、\(x\)軸には、赤い矢印で、だいたいの位置を示します。
すると、以下のようになるのですが、ディノさん、いかがですか?
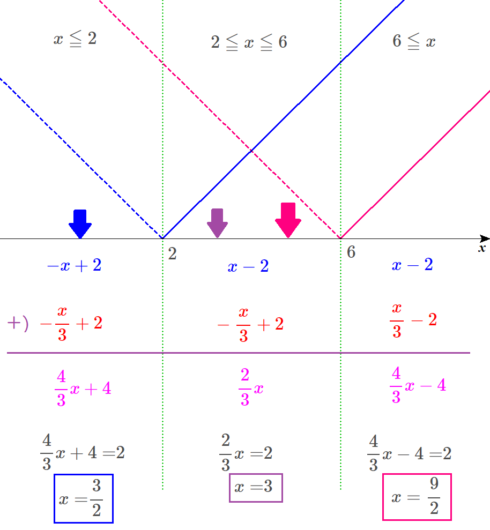

ディノ
おっ、今回は、右の赤い矢印が真ん中の範囲に飛び出してきてるな。
ということは、\(x=\frac{9}{2}\)は、解としては不適ということか?
ということは、\(x=\frac{9}{2}\)は、解としては不適ということか?

Lukia
そのとおりです。

ディノ
なんか、楽勝になってきたな。
こたえ
$$\Large \vert x-2 \vert+\vert \frac{x}{3}-2 \vert=2$$
$$\Large x=\frac{3}{2} , x=3$$
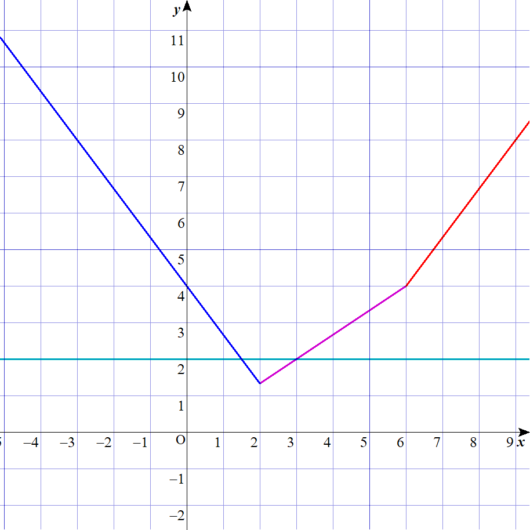

Lukia
実際のグラフは上のようになります。
青の線(左の範囲)と、紫の線(真ん中の範囲)は、\(y=2\) と交わっていますが、
赤い線(右の範囲)は、緑の線のはるか上にあって、まったく交わっていませんね。
青の線(左の範囲)と、紫の線(真ん中の範囲)は、\(y=2\) と交わっていますが、
赤い線(右の範囲)は、緑の線のはるか上にあって、まったく交わっていませんね。
お世話にならせてくださいッ!


Lukia
いや~、ディノさん、すっかり解けるようになったじゃないですかぁ。

ディノ
そうだなぁ。図で考えるとか、一定の手順を踏むって大事だな。

Lukia
私も、お力になれてうれしいです。
それに、お肉やら、パフェやらすっかりごちそうになっちゃって。
ありがとうございました。
それでは、すっかり暗くなってきましたし、このへんで。
それに、お肉やら、パフェやらすっかりごちそうになっちゃって。
ありがとうございました。
それでは、すっかり暗くなってきましたし、このへんで。

ディノ
なに言ってんだよ~。
うち、泊まってけよ~。
ほら、かーちゃんにも会わせたいし。
うち、泊まってけよ~。
ほら、かーちゃんにも会わせたいし。

Lukia
ええっ?

ディノ
教えてもらった恩は、きっちり返す主義なんだ。
それに、ここいらの夜、野宿は危険だぞ?
なんせ、虫とかもデカイからな。
それに、ここいらの夜、野宿は危険だぞ?
なんせ、虫とかもデカイからな。

Lukia
へっ、いかほどの大きさで・・・(汗)

ディノ
う~ん、オマエよりちょっとデカイぐらいかな。
ここらへん、あったかいだろ?
だから、虫もでっかくなっちゃうんだよな。
ここらへん、あったかいだろ?
だから、虫もでっかくなっちゃうんだよな。

Lukia
ひえぇ~~~、お世話になります。
いえっ、お世話にならせてくださいッ!
いえっ、お世話にならせてくださいッ!

ディノ
おっしゃ、じゃ、かーちゃんに「線」しとくわ。

Lukia
「線」って・・・。
なぜか、不思議な世界に一泊することになってしまいました。
まだまだ、ディノさんと問題を解かねばならないようです。









ディスカッション
コメント一覧
まだ、コメントがありません