2019年大学入試センター試験数学1A「第2問データの分析（箱ひげ図とヒストグラム）」を解いてみる。

2019年2月14日2023年1月14日データの分析,大学入試センター試験実用数学技能検定（数学検定数検),数検準2級

読了時間: 約3分48秒

[mathjax]

問題

全国各地の気象台が観測した「ソメイヨシノ（桜の種類）の開花日」や,「モンシロチョウの初見日（初めて観測した日）」,「ツバメの初見日」などの日付を気象庁が発表している。気象庁発表の日付は普通の月日形式であるが、
この問題では該当する年の1月1日を「1」とし,12月31日を「365」（うるう年の場合は「366」）とする「年間通し日」に変更している。例えば,2月3日は,1月31日の「31」に2月3日の3を加えた「34」となる。

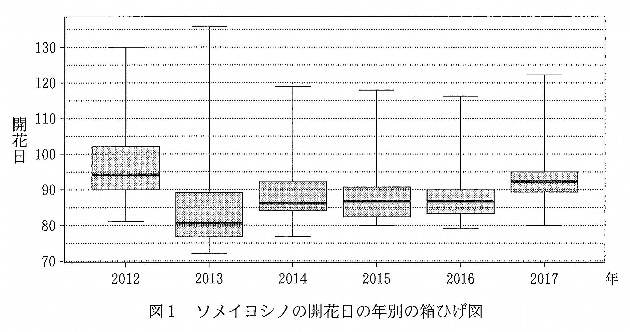
(1)　図1は全国48地点で観測しているソメイヨシノの2012年から2017年までの6年間の開花日を,年ごとに箱ひげ図にして並べたものである。

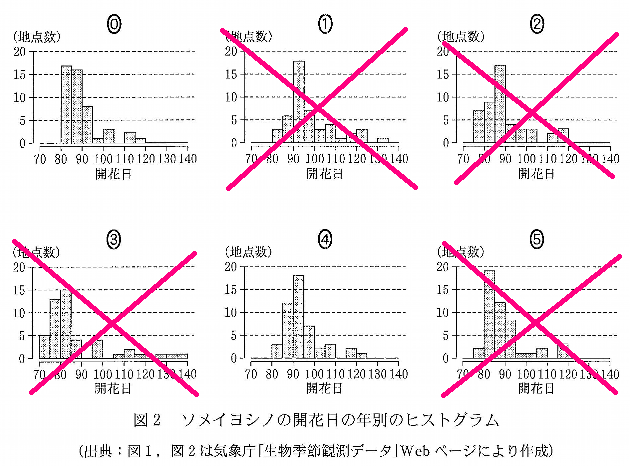
図2はソメイヨシノの開花日の年ごとのヒストグラムである。ただし,順番は年の順に並んでいるとは限らない。なお,ヒストグラムの各階級の区間は,左側の数値含み,右側の数値を含まない。

・　2013年のヒストグラムは$ \ \color{#0004fc}{ソ} \ $である。
・　2017年のヒストグラムは$ \ \color{#0004fc}{タ} \ $である。

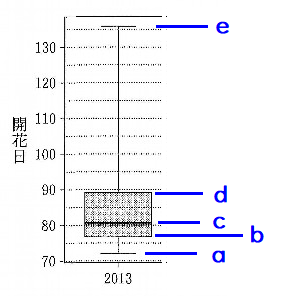
2013年の箱ひげ図から読み取れること。

Lukia

私は、箱ひげ図は「ざっくりと25％ずつがどのように散らばっているかが示されている図」と理解しています。
以下に2013年の箱ひげ図を取り出してみます。

Lukia

まず、$ \ a \ – \ e \ $間が桜の開花が観測された日です。
おおよそですが、72日ごろから131日ごろまでに咲いたことがわかります。

Lukia

次に、
$ \ a \ – \ b \ $間,　$ \ b \ – \ c \ $間,　$ \ c \ – \ d \ $間,　$ \ d \ – \ e \ $間　を見ていきます。
これは、全観測地点が48地点ということですので、それぞれの区間には12地点ずつ含まれていることになりますね。
箱ひげ図では、$ \ c \ $のラインがひときわ太くなっていますが、ここが中央値です。
上から数えても、下から数えてもちょうど真ん中ということになりますね。
ヒストグラムは、度数（今回だと地点数）が正確なのに対し、箱ひげ図はややアバウトです。
しかし、全体の25％（12地点）、50％（24地点）、75％（36地点）が何日までに咲いているか。などが読み取れれば、ヒストグラムと対応させることは可能ですね。

箱ひげ図から読み取れることは以下のとおりである.
最長開花日が135～140日の間にある.
最短開花日が70～75日の間にある.
70～80日の間で24地点が開花している.
70～90日の間で36地点が開花している.

Lukia

この4つの条件から、ヒストグラムをしぼりこんでいきます。
全体として、左側に長い帯が集中しているものになりそうですね。

Lukia

まず、開花日の最長が箱ひげ図では、135～140日の間にありますので、
ヒストグラムとしては、130～140日の間に帯が存在するものでなくてはなりませんね。
これによって①か③にしぼられます。
以下は、①と③のヒストグラムだけを示します。

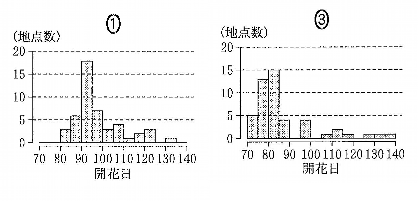
Lukia

次に、最短の開花日を見ていきます。
箱ひげ図では、70～75日の間に最短の開花日がありましたから、ヒストグラムでは70～80日の間に帯がある必要がありますね。
よく見ると、①のヒストグラムには、70～80日の間に帯がありません。
よって、2013年のヒストグラムは,$ \ \color{#0004fc}{③} \ $ということになります。

Lukia

開花日の最短・最長の条件だけですんなり割り出せてしまいましたが、
もう少し確認しておくと、70～90日までで36地点が開花しているんでしたよね。
ヒストグラムは度数（地点数）が5ずつで区切られているので、$ \ 5\cdots10\cdots15\cdots20\cdots \ $と数えてみると、確実に36以上になりそうな度数であることがわかります。

2017年の箱ひげ図から読み取れること。

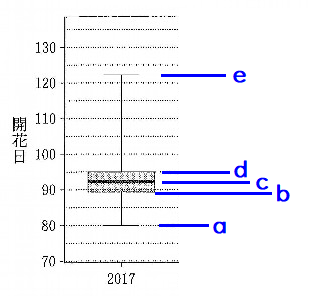
開花日の最短は, 80～85 日ごろであるので,80～90日から始まるヒストグラムである.
開花日の最長は,120～125日ごろであるので,120～130日に度数が存在するヒストグラムである.
12地点は,80～90日までに開花し,
24地点は,80～95日までに開花し,
36地点は,80～95日までに開花するので,80～95日までに度数が36以上存在するヒストグラムである.

Lukia

まず、2013年のヒストグラムを推定する段階で、開花日の最短・最長の条件から、①と③のヒストグラムを除外することができますね。

Lukia

次に最短の開花日を見ると、80日以前に開花しているヒストグラムを除外することができます。
ゆえに,②と⑤が除外となりますね。

Lukia

⓪と④のヒストグラムが残っているわけですが、二つのヒストグラムの大きな違いは、80～85日の度数ですね。
箱ひげ図では、80～90日で少なくとも12地点は開花しているとわかるのですが、⓪のヒストグラムでは、80～85日で15地点以上開花していることになっています。
ゆえに,2017年のヒストグラムは,$ \ \color{#0004fc}{④} \ $だとわかります。