高校数学の「二次関数(の応用?)」問題を解いてみる。(Yahoo!知恵袋より)

2点\( \ \mathrm{A} \ , \ \mathrm{B} \ \)はともに曲線①上の点で、点\( \ \mathrm{A} \ \)の\( \ x \ \)座標は\( \ -4 \ \)であり,線分\( \ \mathrm{AB} \ \)は\( \ x \ \)軸に平行である。また,点\( \ \mathrm{C} \ \)は曲線②上の点で,線分\( \ \mathrm{BC} \ \)は\( \ y \ \)軸に平行である。点\( \ \mathrm{D} \ \)は線分\( \ \mathrm{BC} \ \)と\( \ x \ \)軸との交点であり,\( \ \mathrm{BD}:\mathrm{DC}=4:1 \ \)である。点\( \ \mathrm{E} \ \)は\( \ y \ \)軸上の点で,その\( \ y \ \)座標は正である。
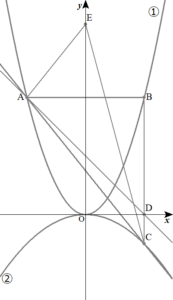
原点を\( \ \mathrm{O} \ \)とするとき,以下の問いに答えなさい。
(1) 曲線②の式の\( \ y=ax^2 \ \)の\( \ a \ \)の値を求めよ。
(2) 直線\( \ \mathrm{AD} \ \)の式を求め,\( \ y=mx+n \ \)の形で示せ。
(3) 三角形\( \ \mathrm{ABC} \ \)と三角形\( \ \mathrm{AEC} \ \)の面積が等しくなるとき,点\( \ \mathrm{E} \ \)の座標を求めよ。
(4) 三角形\( \ \mathrm{AEC} \ \)が\( \ \angle \mathrm{EAC}=90^{\circ} \ \)の直角三角形となるとき,点\( \ \mathrm{E} \ \)の座標を求めよ。
[mathjax]
(1)を解く。
$$\begin{align}点\mathrm{B}は&y \ 軸に関して \ 点\mathrm{A} \ と対称であるから, \\\\ \mathrm{B}&\left( 4 \ , \ 8\right)\quad である. \\\\ \mathrm{D}&\left( 4 \ , \ 0\right) \quad ,\quad \mathrm{C}\left( 4 \ , \ 16a\right)\quad と表せる.\\\\ &\mathrm{BD}:\mathrm{DC}=4:1
=8:-16a\quad より\\\\ a=&-\frac{1}{8} \end{align}$$
(2)を解く。
$$\begin{align}\mathrm{A}&\left( -4 \ , \ 8\right) \quad \mathrm{D}\left( 4 \ , \ 0\right)\quad であるから,\\\\ y=&\frac{0-8}{4+4}\left( x-4\right) \\\\ y=&-x+4 \end{align}$$
(3)を解く。
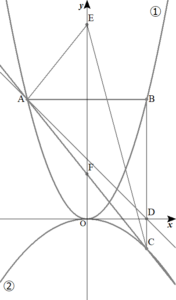
$$\begin{align}\triangle \mathrm{ABC}&の面積を \ \mathrm{S}_1 \ とする. \\\\ \mathrm{S}_1=&\frac{1}{2}\times \vert \mathrm{AB} \vert\vert \mathrm{BC} \vert \\\\ =&\frac{1}{2}\times 8\times 10=40 \end{align}$$
$$\begin{align}ここで,&直線\mathrm{AC} \ は, \\\\ y=&-\frac{5}{4}x+3\quad であり, \\\\ 直線\mathrm{AC}&と \ y \ 軸との交点を\mathrm{F}とすると,\\\\ \mathrm{F}&\left( 0 \ , \ 3\right)\quad である. \end{align}$$
$$\begin{align}点\mathrm{E}&を\left( 0 \ , \ e\right)\quad \left( e \gt 0\right) \ とし,\\\\ \triangle \mathrm{AEC}&の面積を \ \mathrm{S}_2 \ とすると, \\\\ \mathrm{S}_2=&\frac{1}{2}\vert \mathrm{EF} \vert \times \left( x_C-x_A\right)\\\\ =&\frac{1}{2}\times \left( e-3\right)\times \left( 4+4\right)=4\left( e-3\right) \end{align}$$
$$\begin{align}\mathrm{S}_1=&\mathrm{S}_2 \\\\ 40=&4\left( e-3\right) \\\\ 10=&e-3\\\\ e=&13\\\\ ゆえに&\quad \mathrm{E}\left( 0 \ , \ 13\right) \end{align}$$
(4)を解く。
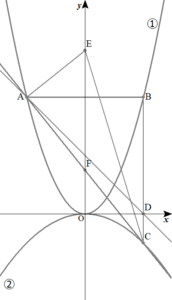
$$\begin{align}\left( 3\right)より \\\\ &直線\mathrm{AC} \ は, \\\\ y=&-\frac{5}{4}x+3\quad であり, \\\\ \mathrm{E}&\left( 0 \ , \ e\right) \quad とする.\\\\ このとき,&直線\mathrm{EA} \ の傾きは,\\\\ &\frac{e-8}{4} \ と表せる. \end{align}$$
$$\begin{align}直線\mathrm{AC}と&直線\mathrm{EA}が垂直に交わるので, \\\\ -\frac{5}{4}\times \left( \frac{e-8}{4}\right)=&-1 \\\\ これを&解いて,\\\\ e=&\frac{56}{5}\\\\ ゆえに&\mathrm{E}\left( 0 \ , \ \frac{56}{5}\right) \end{align}$$
こたえ
$$\begin{align}\left( 1\right)\quad &a=-\frac{1}{8} \\\\ \left( 2\right)\quad &y=-x+4 \\\\ \left( 3\right)\quad &\mathrm{E}\left( 0 \ , \ 13\right)\\\\ \left( 4\right)\quad &\mathrm{E}\left( 0 \ , \ \frac{56}{5}\right) \end{align}$$
[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません