高校数学の「データの分析（相関係数）」に関する問題を解いてみる。（Yahoo!知恵袋より）

2019年4月9日2023年1月14日データの分析実用数学技能検定（数学検定 数検),数検準2級

[mathjax]

$$\begin{align}個々のデータを\quad &x_i \ , \ y_i\quad \left( i=1 \ , \ 2 \ , \ \cdots \ , \ 10\right) \quad とし,\\\\ 平均を\quad &\overline{x} \ , \ \overline{y} \\\\ 分散を\quad &s_x^2 \ , \ s_y^2\\\\ 共分散を\quad &s_{xy}\\\\ 相関係数を\quad &r\quad とする. \end{align}$$

$$\begin{align}\overline{x}=&\frac{1}{10}\sum_{i=1}^{10}{x_i}=110 \\\\ \overline{y}=&\frac{1}{10}\sum_{i=1}^{10}{y_i}=44 \\\\ s_x^2=&\frac{1}{10}\sum_{i=1}^{10}{\left( x_i-\overline{x}\right)^2}=75\\\\s_y^2=&\frac{1}{10}\sum_{i=1}^{10}{\left( y_i-\overline{y}\right)^2}=147 \\\\ s_{xy}=&\frac{1}{10}\sum_{i=1}^{10}{\left( x_i-\overline{x}\right)\left( y_i-\overline{y}\right)}=-87.5 \end{align}$$

$$\begin{align}r=&\frac{s_{xy}}{\sqrt{s_x^2}\sqrt{s_y^2}} \\\\ =&\frac{-87.5}{\sqrt{75\times 147}} \\\\ =&-0.83333\cdots\ =&-0.83 \end{align}$$

Lukia

以下に示す分布図は、横軸を\( \ x \ \), 縦軸を\( \ y \ \)としたものです。

Lukia

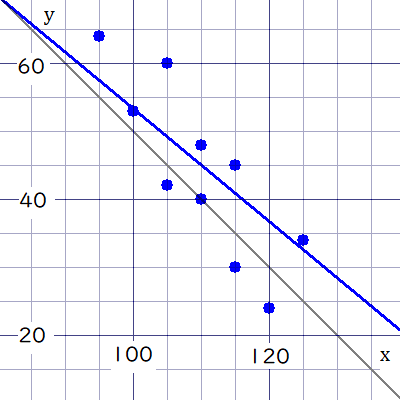
10個の点は、全体的に右下がりになるような分布となっていますね。

灰色の線は相関係数が\( \ -1 \ \)の場合を示します。
灰色の線は、「値段が高くなるほど、例外なく販売数が減る」ということを示しています。
要するに、「高いと売れない。」といえるのです。

Lukia

いっぽう、青い線は、求めた相関係数\( \ -0.83 \ \)の場合を示しています。
右下がりであることは間違いないものの、灰色の線に比べると、傾きがややゆるやかですね。これは、同じ値段でも、よく売れたもの、あまり売れなかったものの差があったり、
値段が高いわりには、まぁまぁ売れるものがあったりしたためです。

Lukia

つまり、
「安いと売れる。高いと売れない。」と断言はできないけれど、
「安いと売れやすく、高いと売れにくい。」というのは、言いすぎじゃない。ということになります。

Lukia

飲料会社の人は、こういうデータを分析していくんでしょうね。
もし市場が灰色の線だったら、消費者が「飲料に好みなど言っていられない。とにかく安いものを！」と考えていることになるので、商品開発というよりは、価格破壊に重点をおくことになります。
しかし、今回の分布図では、消費者は、たしかに価格が高いと買わなくなるけれど、商品に魅力があれば買ってくれる場合もある。ということを示すので、
「魅力のある商品を適切な価格で売れるように開発すること」が、メーカーの課題ということになります。

こたえ

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。