高校数学の「ふたつの実数がなす範囲」に関する問題を解いてみる。（Yahoo!知恵袋より）

2019年3月1日2023年1月14日数と式実用数学技能検定（数学検定 数検),数検準2級

[mathjax]

$$\begin{align}(1)\quad &小数第一位を四捨五入すると \ 3 \ になる正の数 \ a \ は, \\ &2.5 \leq a \leq 3.4\end{align}$$

$$\begin{align}(2)\quad 小数第一位を四捨五入すると &\ 5 \ になる正の数 \ b \ は, \\ &4.5 \leq a \leq 5.4\quad である.\\ a+bの存在範囲は, &a \ と \ b \ の最小値の和から \\ &\ a \ と \ b \ の最大値の和までの範囲に相当するから,\\ &2.5+4.5 \leq a+b \leq 3.4+5.4\\ &7.0 \leq a+b \leq 8.8 \end{align}$$

Lukia

(3)　は、\( \ a+\color{#0004fc}{\left( -b\right)} \ \)として考えます。

$$\begin{align}(3)\quad &\color{#0004fc}{-5.4 \leq -b \leq -4.5}\quad であるから, \\ &2.5+\color{#0004fc}{\left( -5.4\right)} \leq a+\color{#0004fc}{\left( -b\right)} \leq 3.4+\color{#0004fc}{\left( -4.5\right)} \\ &-2.9 \leq a-b \leq -1.1 \end{align}$$

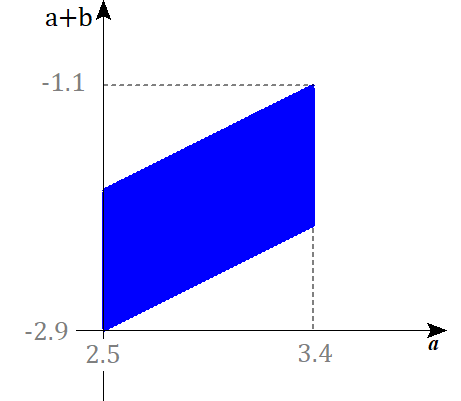
こたえ

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。