高校数学の「平面ベクトル（ある媒介変数の最小値）」に関する問題を解いてみる。（Yahoo!知恵袋より）

2019年2月18日2023年1月14日ベクトル実用数学技能検定（数学検定 数検),数検2級,数検準1級

[mathjax]

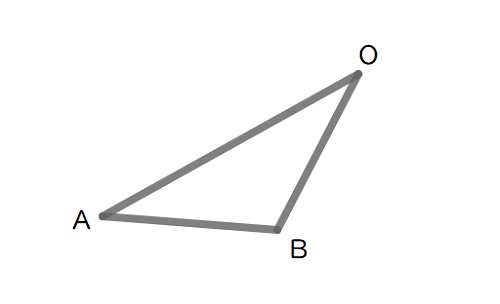
ベクトルの問題は図をかかなきゃ始まらない。

Lukia

上の図のような\( \ \triangle \mathrm{OAB} \ \)を想定すると,
\( \ \overrightarrow{\mathrm{OA}}=\vec{a} \ \),\( \ \overrightarrow{\mathrm{OB}}=\vec{b} \ \),\( \ \overrightarrow{\mathrm{BA}}=\vec{a}-\vec{b} \ \)と表せます。

$$\begin{align}\vert \vec{a}+t\vec{b} \vert^2=&\vert \vec{a} \vert^2+2t\vec{a}\cdot \vec{b}+t^2\vert \vec{b} \vert^2\quad \cdots\cdots\quad ★ \\\\ ここで,\quad \cos \angle \mathrm{AOB}=&\frac{\vec{a}\cdot \vec{b}}{\vert \vec{a} \vert　\vert \vec{b} \vert}=\frac{\vec{a}\cdot \vec{b}}{15}\quad \cdots\quad ① \\\\ また,\triangle \mathrm{OAB}&\quad について余弦定理より\\\\ \cos \angle \mathrm{AOB}=&\frac{5^2+3^2-3^2}{2\cdot 5\cdot 3}=\frac{5}{6}\quad \cdots\quad ②\\\\ ① \ = \ ②\quad &より\\\\ \vec{a}\cdot \vec{b}=&\frac{25}{2} \end{align}$$
★に代入して,
$$\begin{align}与式=&25+2t\cdot \frac{25}{2}+9t^2 \\\\ =&9t^2+25t+25 \\\\ f\left( t\right)=&9t^2+25t+25\quad とすると,\\\\ f\left( t\right)\quad が&最小となるのは,\quad t=-\frac{25}{18}\quad のとき. \end{align}$$

ちなみに。

Lukia

問題は、\( \ t \ \)の値を求めるところで終わっていますが、
実際にいくらになるのか、考えてみましょう。

$$\begin{align}\vert \vec{a}+t\vec{b} \vert^2=&f\left( t\right)=9t^2+25t+25\quad より \\\\ \vert \vec{a}+t\vec{b} \vert\quad &の最小値は, \\\\ \sqrt{f\left( -\frac{25}{18}\right)}=&\sqrt{\frac{25\times 11}{36}} =\frac{5}{6}\sqrt{11}\end{align}$$

こたえ

$$t=-\frac{25}{18}$$

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。