Yahoo!知恵袋の高校数学カテゴリにあった「積分とその応用」に関する問題を解いてみる。

2018年10月7日2023年1月15日積分とその応用実用数学技能検定（数学検定 数検),数検準1級

解法

$$\begin{align}\log x=&t とする。\\\\ また、x=&e^t \\\\両辺をxで微分すると \frac{1}{x}=&\frac{dt}{dx} \\\\ dx=&xdt より、\end{align}$$
$$I=\int \cos t\cdot e^t dt $$
とあらわせる。

Lukia

以下は「テーブル法」といわれるもののようですが、
入試や定期テストなどの解答には書かないでください。
いってみれば裏技なので、書くとバツされちゃいます。

Lukia

片方を微分、片方を積分します。
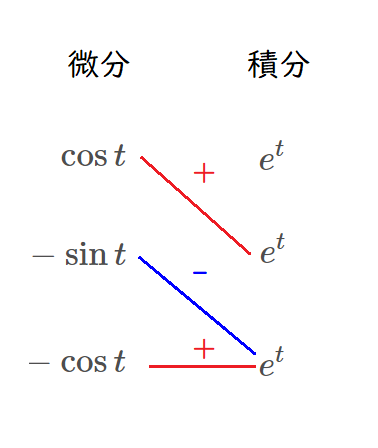
今回は、\(\cos t\)を微分、\(e^t\)を積分します。
次に、微分とその1段下の積分を積でつなぎます。
一番下は、横につないでいますが、ここは積分の記号インテグラルを書きます。
赤い線は、+（プラス）で、青の線は-（マイナス）でつなげます。

$$\begin{align}\int \cos t\cdot e^t dt=&\cos t\cdot e^t\color{blue}{-}\left( -\sin t\cdot e^t\right)\color{red}{+}\int\left( -\cos t\cdot e^t\right) dt \\\\ \color{blue}{\int \cos t\cdot e^t dt}=&\cos t\cdot e^t+\sin t\cdot e^t-\color{blue}{\int \cos t\cdot e^t dt} \\\\ \color{blue}{2\int \cos t\cdot e^t dt}=&\cos t\cdot e^t+\sin t\cdot e^t+\mathrm{C}\\\\ \int \cos t\cdot e^t dt=&\frac{1}{2}\left( \cos t\cdot e^t+\sin t\cdot e^t\right)+\mathrm{C} \end{align}$$

Lukia

\(t\)は、私が勝手においたものなので、ふたたび\(x\)に置換しなおします。

$$\begin{align}I=\int \cos t\cdot e^t dt=&\frac{1}{2}\left( \cos t\cdot e^t+\sin t\cdot e^t\right)+\mathrm{C} \\\\ =&\frac{x}{2}\left( \cos \left( \log x\right)+\sin \left( \log x\right)\right)+\mathrm{C}\\\\ &\left( ただし、\mathrm{C}は積分定数\right) \end{align}$$

こたえ

$$\frac{x}{2}\left( \cos \left( \log x\right)+\sin \left( \log x\right)\right)+\mathrm{C}$$

(ただし、Cは積分定数）

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。