高校数学の「内分線に囲まれた三角形の面積」に関する問題を解いてみる。（Yahoo!知恵袋より）

2019年2月9日2023年1月14日図形と計量実用数学技能検定（数学検定 数検),数検準2級

[mathjax]

内分比を統一していこう。

Lukia

内分比を、反対側の頂点に互い違いにおいていくことで、
最終的には内分比の統一をめざします。
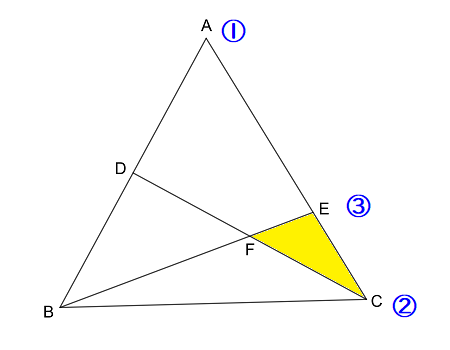
まず、辺\( \ \mathrm{AC} \ \)を\( \ 2：1 \ \)に内分するので、
頂点\( \ \mathrm{C} \ \)に②をおき、
頂点\( \ \mathrm{A} \ \)に①をおきます。
そして、点\( \ \mathrm{E} \ \)は内分比の和である③をおきます。

Lukia

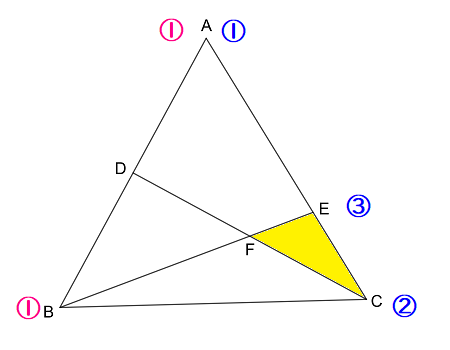
同様に辺\( \ \mathrm{AB} \ \)の内分比も書き込みます。
辺\( \ \mathrm{AB} \ \)は、点\( \ \mathrm{D} \ \)によって、\( \ 1：1 \ \)に内分されますね。
それぞれの頂点に①を書き込むわけですが、頂点\( \ \mathrm{A} \ \)にはすでに①があります。
実際には、\( \ \color{#0004fc}{①}\times \color{#f700ca}{①} \ \)が行われることになるのですが、見た目には区別がつかないので、
①で統一していきます。

Lukia

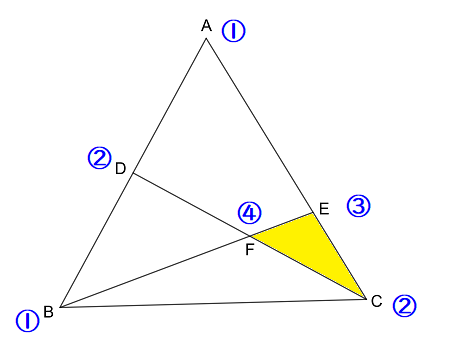
内分比を統一したのが、以下の図です。
すると、2本の線分の交点\( \ \mathrm{F} \ \)にも、内分比がつけられますね。

Lukia

点\( \ \mathrm{F} \ \)は線分\( \ \mathrm{BE} \ \)を\( \ 3:1 \ \)に内分するといえますね。

ここまで導いたら、あとは段階をふんで表現していくだけです。

$$\begin{align}\triangle \mathrm{ABC}の面積を\mathrm{S}&とする. \\\\ \mathrm{S}=&\frac{1}{2}12^2\sin 60^{\circ} \\\\ =&36\sqrt{3} \end{align}$$
$$\begin{align}\triangle \mathrm{EBC}=&\frac{1}{3}\triangle \mathrm{ABC} \\\\ \triangle \mathrm{EFC}=&\frac{1}{4}\triangle \mathrm{EBC} \\\\ =&\frac{1}{12}\triangle \mathrm{ABC}\\\\ =&3\sqrt{3} \end{align}$$

こたえ

$$3\sqrt{3}$$

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。