高校数学の「図形と計量(角の二等分線がらみ)」に関する問題を解いてみる。(Yahoo!知恵袋より)

[mathjax]
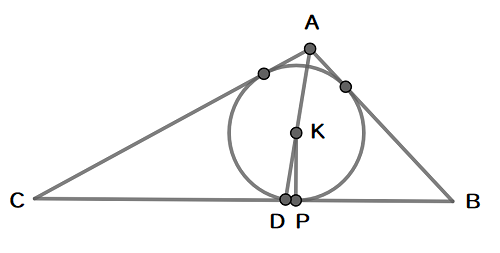
内心を点\( \ \mathrm{K} \ \)とする。
内接円と\( \ \mathrm{BC} \ \)の接点を\( \ \mathrm{P} \ \)とする。
\( \ \mathrm{BC} \ \)と\( \ \mathrm{AK} \ \)の交点を\( \ \mathrm{D} \ \)とする。
(1) \( \ \cos \angle \mathrm{BAC} \ \)を求めよ。
(2) 三角形\( \ \mathrm{ABC} \ \)の面積を求めよ。
(3) \( \ \mathrm{PK} \ \)の長さを求めよ。
(4) 三角形\( \ \mathrm{KPD} \ \)の面積を求めよ。
$$\begin{align}(1)\quad \quad \cos \angle \mathrm{BAC}=&\frac{6^2+4^2-8^2}{2\cdot 6\cdot 4} =-\frac{1}{4}\\\\(2)\quad \quad (1)より\sin \angle \mathrm{BAC}=&\frac{\sqrt{15}}{4}\\\\ \quad \quad \mathrm{S}=&\frac{1}{2}\cdot 6\cdot 4\cdot \frac{\sqrt{15}}{4}=3\sqrt{15} \end{align}$$
$$\begin{align}(3)\quad \quad \mathrm{S}=&\frac{1}{2}\left( \mathrm{AB}+\mathrm{BC}+\mathrm{CA}\right)\cdot \mathrm{KP} \\\\ 3\sqrt{15}=&20\mathrm{KP} \\\\ \mathrm{KP}=&\frac{3\sqrt{15}}{10} \end{align}$$

Lukia
円に外接する三角形のそれぞれの角の二等分線の交点でもあります。
そして、角の二等分線は、対辺を角をなす2本の線分の比に内分します。
$$\begin{align}線分 \ \mathrm{AD}\quad は&辺 \ \mathrm{CB}\quad を \ 3:2\quad に内分する. \\\\ \mathrm{DB}=&\frac{2}{5}\times 8=\frac{16}{5} \\\\ また \ \mathrm{PB}=&3\quad より\\\\ \mathrm{DP}=&\frac{1}{5}\\\\ \triangle \mathrm{KDP}=&\frac{1}{2}\times \mathrm{DP}\times \mathrm{PK}=\frac{3\sqrt{15}}{100} \end{align}$$
[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません