高校数学の「二次関数が解をもつ条件・軌跡」に関する問題を解いてみる。（Yahoo!知恵袋より）

2019年1月31日2023年1月14日二次関数実用数学技能検定（数学検定 数検),数検準2級

[mathjax]

わかっていることを視覚化してみる。

Lukia

問題の形式からすると,大学入試センター試験対策の問題のようでもありますね。
虫食いになっていない部分から ある程度答えを絞り込めるのが、マーク式タイプの問題のいいところです。

Lukia

問題文によって、グラフ\( \ \mathrm{C} \ \)に関する情報がある程度得られますね。
★　\( \ \mathrm{C} \ \)は上に凸の放物線である.
☆　異なる2つの実数解をもつことから、\( \ \mathrm{C} \ \)の頂点の\( \ y \ \)座標は正である.
★　\( \ \mathrm{C} \ \)と\( \ x \ \)軸は、\( \ x \lt -2 \ \)または\( \ 2 \lt x \ \)の範囲で交わる.

Lukia

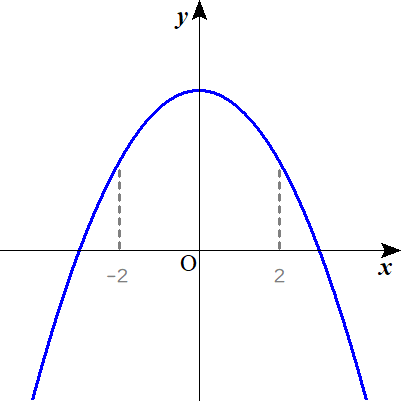
そして、この情報をもとにグラフ\( \ \mathrm{C} \ \)の概形を描くと以下の図のようになります。

また、「概形（だいたいの形）」とことわっているように、
軸は、\( \ y \ \)軸で固定ではありません。
少なくとも\( \ -2 \lt 軸 \lt 2 \ \)を満たしていればいいことになります。

Lukia

図にしたことで、さらにわかることがありますね。
\( \ \mathrm{C} \ \)を\( \ y=f\left( x\right) \ \)とおいたとき,
\( \ f\left( -2\right) \gt 0 \ \)かつ\( \ f\left( 2\right) \gt 0 \ \)ということです。

$$\begin{align}y=&f\left( x\right)\quad とおく. \\\\ グラフより,\quad f\left( -2\right) \gt &0\quad かつ\quad f\left( 2\right) \gt 0\quad であるので, \\\\ f\left( -2\right)=&\left( a-2\right)^2 \gt 0\\\\ &a\quad は \ 2 \ 以外のすべての実数\quad \cdots\cdots\quad ①\\\\ f\left( 2\right)=&\left( a+2\right)^2-24 \gt 0\\\\ &-2-2\sqrt{6} \lt a \ , \ -2+2\sqrt{6} \lt a\quad \cdots\cdots\quad ②\\\\ \ ① \ , \ ② \ より&a \lt -\color{#0004fc}{2}-\color{#0004fc}{2}\sqrt{\color{#0004fc}{6}} \ , \ -\color{#0004fc}{2}+\color{#0004fc}{2}\sqrt{\color{#0004fc}{6}} \lt a \end{align}$$

頂点の座標は機械的に求められるようにしておこう。

$$\left( \frac{a-\color{#0004fc}{3}}{\color{#0004fc}{2}} \ , \ \frac{\color{#0004fc}{3}a^2-\color{#0004fc}{6}a+\color{#0004fc}{9}}{\color{#0004fc}{2}}\right)$$

頂点の軌跡を求める。

$$\begin{align}グラフ\mathrm{C}の&頂点の座標は \\\\ \left( x \ , \ y\right)=&\left( \frac{a-3}{2} \ , \ \frac{3a^2-6a+9}{2}\right) \\\\ 2x=&a-3\quad すなわち\quad a=2x+3\\\\ y=&\frac{3}{2}\left( a^2-2a+3\right)=\frac{3}{2}\lbrace \left( a-1\right)^2+2\rbrace\\\\ =&\frac{3}{2}\lbrace \left( 2x+3-1\right)^2+2\rbrace=\frac{3}{2}\left( 2x+2\right)^2+3\\\\ =&\frac{3}{2}\cdot 2^2\left( x+1\right)^2+3\\\\ =&6\left( x+1\right)^2+3=\color{#0004fc}{6}x^2+\color{#0004fc}{12}x+\color{#0004fc}{9} \end{align}$$

こたえ

$$\begin{align}\left( 1\right)\quad &a \lt -\color{#0004fc}{2}-\color{#0004fc}{2}\sqrt{\color{#0004fc}{6}} \ , \ -\color{#0004fc}{2}+\color{#0004fc}{2}\sqrt{\color{#0004fc}{6}} \lt a \\\\ \left( 2\right)\quad &\left( \frac{a-\color{#0004fc}{3}}{\color{#0004fc}{2}} \ , \ \frac{\color{#0004fc}{3}a^2-\color{#0004fc}{6}a+\color{#0004fc}{9}}{\color{#0004fc}{2}}\right) \\\\ \left( 3\right)\quad &y=\color{#0004fc}{6}x^2+\color{#0004fc}{12}x+\color{#0004fc}{9} \end{align}$$

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。