高校数学の「絶対値記号を含む積分」に関する問題を解いてみる。（Yahoo!知恵袋より）
問題
$$fleft( aright)=int_{0}^{1} vert left( x-1right)left( x-aright) vert dxquad left( a geq 0right)$$
で定義するとき, (fleft( aright))を ( a )の式で表せ.
$$begin{align}mathrm{F}left( xright)=&int left( x-1right)left( x-aright) dx とする. \\ \\ mathrm{F}left( xright)=&frac{1}{3}x^3-frac{left( a+1right)}{2}x^2+ax+mathrm{C}quad left( mathrm{C}は積分定数right) end{align}$$
ⅰ） a=0 のとき
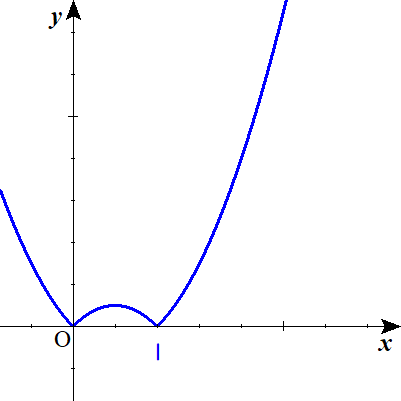
$$begin{align}fleft( aright)=&-int_{0}^{1} left( x-1right)left( x-aright) dx \\ =&-mathrm{F}left( 1right)+mathrm{F}left( 0right) \\ =&frac{1}{6} end{align}$$
ⅱ） 0＜a＜1 のとき
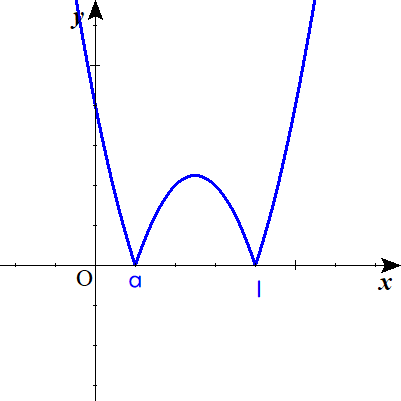
$$begin{align}fleft( aright)=&int_{0}^{a} left( x-1right)left( x-aright) dx-int_{a}^{1} left( x-1right)left( x-aright) dx \\ =&2mathrm{F}left( aright)-mathrm{F}left( 1right)-mathrm{F}left( 0right) \\ =&-frac{1}{3}a^3+a^2-frac{a}{2}+frac{1}{6} end{align}$$
ⅲ） a=1 のとき
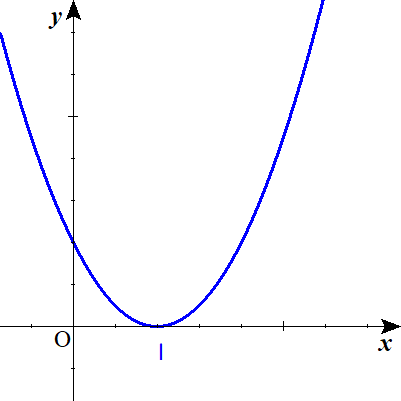
$$begin{align}fleft( aright)=&int_{0}^{1} left( x-1right)^2 dx \\ =&frac{1}{3}end{align}$$
ⅳ） a＞1 のとき
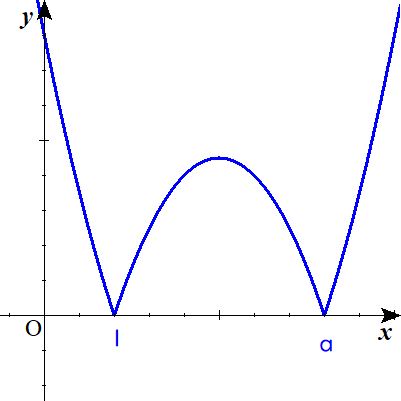
$$begin{align}fleft( aright)=&int_{0}^{1} left( x-1right)left( x-aright) dx \\ =&mathrm{F}left( 1right)-mathrm{F}left( 0right) \\ =&frac{3a-1}{6} end{align}$$
Lukia
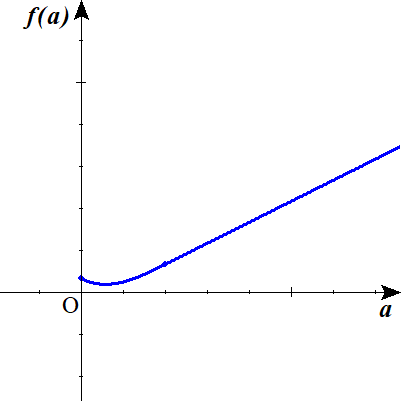
( 0 leq a leq 1 )は曲線となり、( 1 lt a )では、右上がりの直線となっています。
こたえ
省略
