高校数学の「現実にはエグい坂と塔」に関する問題を解いてみる。【Yahoo!知恵袋より】
読了時間: 約2分32秒
Yahoo!知恵袋の高校数学カテゴリに掲載されていた「現実にはエグい坂と塔」に関する問題を解いてみました。
問題
傾斜が\( \ 30^{\circ} \ \)で一定の坂の頂上に塔が立っている。坂のふもとからこの塔の先を見ると、水平面に対して\( \ 45^{\circ} \ \)の角度に見えた。坂を斜面に沿って塔に向かって\( \ 30 \ \)m進んだ\( \ \mathrm{A} \ \)点から再び塔の先を見ると、水平面に対して\( \ 60^{\circ} \ \)の角度に見えた。
1） \( \ \mathrm{A} \ \)点から坂の頂上まで、斜面に沿ってさらに何mあるか。
2） 塔そのものの高さは何mであるか。
3） 塔の先と坂のふもとの高低差は何mであるか。 〔03 朝日大〕
1） \( \ \mathrm{A} \ \)点から坂の頂上まで、斜面に沿ってさらに何mあるか。
2） 塔そのものの高さは何mであるか。
3） 塔の先と坂のふもとの高低差は何mであるか。 〔03 朝日大〕
解法
坂の頂上まであと○m
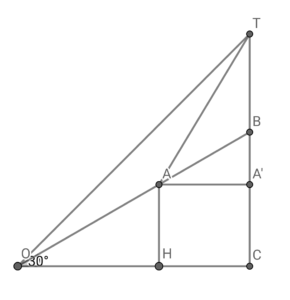\( \ \triangle \mathrm{AOH} \ \) において、\( \ \mathrm{AO}=30 \ \) より、\( \ \mathrm{AH}=15\sqrt{3} \ \) , \( \ \mathrm{AH}=15 \ \) である。
ここで、\( \ \mathrm{AA’}=\mathrm{HC}=x \ \) とする。
\( \ \triangle \mathrm{TAA’} \ \) において、\( \ \mathrm{TA’}=\sqrt{3}x \ \)である。
\( \ \triangle \mathrm{TOC} \ \) において、\( \ \mathrm{OC}=\mathrm{TC} \ \) より
$$\begin{align}\mathrm{OC}=&\mathrm{TC} \\\\ 15\sqrt{3}+x=&15+\sqrt{3}x \\\\ x\left( 1-\sqrt{3}\right)=&15\left( 1-\sqrt{3}\right) \\\\ x=&15\end{align}$$
\( \ \triangle \mathrm{BAA’} \ \) において \( \ \mathrm{AB}:\mathrm{AA’}=2:\sqrt{3} \ \) より
\( \ \mathrm{AB}=10\sqrt{3} \ \) (m)
塔の高さは○m
塔の高さを\( \ t \ \) とする（\( \ t \ \) は実数） \( \ \triangle \mathrm{TAA’} \ \) において$$\begin{align}\mathrm{AA’}:\mathrm{A’T}=& 15:\left( t+5\sqrt{3}\right)=1:\sqrt{3}\\\\ 15\sqrt{3}=&t+5\sqrt{3} \\\\ t=& 10\sqrt{3} \ \left( \rm{m}\right)\end{align}$$
塔のてっぺんまでの高さ
\( \ \triangle \mathrm{TOC} \ \)において\( \ \mathrm{TC}=\mathrm{OC} \ \) より\( \ 15\left( \sqrt{3}+1\right) \ \) (m)
図を描いているときからなんだかエグそうな坂や塔だなと思っていたんですよね。
そこで、実際に計算してみました。
坂の頂上まで\( \ 47 \ \)mですから、\( \ 50 \ \)m走ができないんです。
\( \ 47 \ \)mしかないのに、\( \ 41 \ \)mも高くなります。
おそらくひっくり返りそうなぐらい急な坂です。登りきったら転げ落ちそうで怖いんじゃないかな。
そして、その坂の上に立つ塔のエグさときたら。
\( \ 17.3 \ \)mもあるんです。
坂のふもとから見たら、塔がど〜ん！と見える感じでしょうね。
そこで、実際に計算してみました。
坂の頂上まで\( \ 47 \ \)mですから、\( \ 50 \ \)m走ができないんです。
\( \ 47 \ \)mしかないのに、\( \ 41 \ \)mも高くなります。
おそらくひっくり返りそうなぐらい急な坂です。登りきったら転げ落ちそうで怖いんじゃないかな。
そして、その坂の上に立つ塔のエグさときたら。
\( \ 17.3 \ \)mもあるんです。
坂のふもとから見たら、塔がど〜ん！と見える感じでしょうね。
共有:
プロフィール
Author Profile