高校数学の「領域と最大値・最小値」に関する問題を解いてみる。【Yahoo!知恵袋より】
読了時間: 約2分47秒
Yahoo!知恵袋の高校数学カテゴリに掲載されていた「領域と最大値・最小値」に関する問題を解いてみました。
問題
座標平面上で、連立不等式
\( \ \begin{eqnarray} \left\{ \begin{array}{l} x^2 + y^2 \leqq 4 \\ \left( x-y+2\right)\left( 2x+y-2\right) \leqq 0 \end{array} \right. \end{eqnarray} \ \)
の表す領域を\( \ \mathrm{D} \ \)とする。
点\( \ \left( x \ , \ y\right) \ \)が領域\( \ \mathrm{D} \ \)を動くとき、
\( \ x+y \ \) の最大値と最小値を求めよ。
解法
領域を定める
領域\( \ \mathrm{D} \ \)を定める。\( \ \left( x-y+2\right)\left( 2x+y-2\right) \leqq 0 \ \) は、
①
\( \ x-y+2 \leqq 0 \ \) かつ \( \ 2x+y-2 \geqq 0 \ \) の場合と
②
\( \ x-y+2 \geqq 0 \ \) かつ \( \ 2x+y-2 \leqq 0 \ \) の場合がある。
——————————————————————————————–
①と\( \ x^2 + y^2 \leqq 4 \ \)が示す領域は以下の図のとおり。
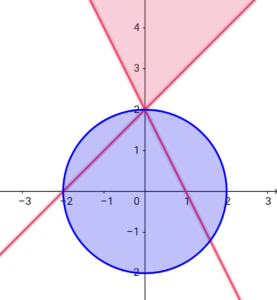重なる領域がほぼ存在しないので、①は不適。②と\( \ x^2 + y^2 \leqq 4 \ \)が示す領域は以下の図のとおり。
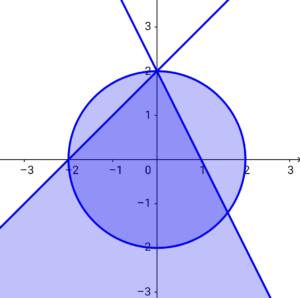
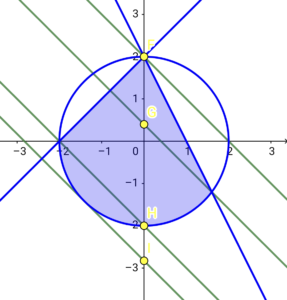
円の内部の濃い青色部分が領域\( \ \mathrm{D} \ \)となる。
ゆえに領域\( \ \mathrm{D} \ \)は、以下の図のとおり。（境界を含む）
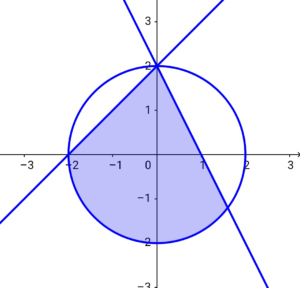
最大値・最小値を求める
\( \ l:x+y=k \ \) （ \( \ k \ \) は実数）とする。\( \ l \ \)を\( \ y=-x+k \ \)と変形すると、切片\( \ k \ \)の最大値・最小値を求めればよいことがわかる。
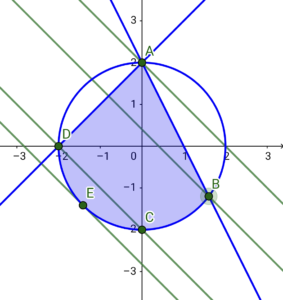
① 点\( \ \mathrm{A}\left( 0 \ , \ 2\right) \ \) を通るとき
② 点\( \ \mathrm{B}\left( \displaystyle\frac{8}{5} \ , \ -\displaystyle\frac{6}{5}\right) \ \) を通るとき
③ 点\( \ \mathrm{C}\left( 0 \ , \ -2\right) \ \) と点\( \ \mathrm{D}\left( -2 \ , \ 0\right) \ \) を通るとき
④ 点\( \ \mathrm{E}\left( -\sqrt{2} \ , \ -\sqrt{2}\right) \ \) を通るときの4通りについて考える。
\( \ k=x+y \ \) であるので、
① \( \ k=0+2=2 \ \) (下図の点\( \ \mathrm{F} \ \) )
② \( \ k=\displaystyle\frac{8}{5}-\displaystyle\frac{6}{5}=\displaystyle\frac{2}{5} \ \) (下図の点\( \ \mathrm{G} \ \) )
③ \( \ k=0-2=-2 \ \) (下図の点\( \ \mathrm{H} \ \) )
④ \( \ k=-\sqrt{2}-\sqrt{2}=-2\sqrt{2} \ \) (下図の点\( \ \mathrm{I} \ \) )
以上より、最大値は\( \ 2 \ \) , 最小値は\( \ -2\sqrt{2} \ \)
こたえ
最大値：\( \ 2 \ \)
最小値：\( \ -2\sqrt{2} \ \)
共有:
プロフィール
Author Profile
