高校数学の「二次関数の総合問題？」を解いてみる。【Yahoo!知恵袋より】
読了時間: 約1分33秒
Yahoo!知恵袋の高校数学カテゴリに掲載されていた「二次関数の総合問題？」を解いてみました。
問題
放物線 \( \ y=2x^2-4x+k \ \cdots \ \ \)①について、次の問いに答えなさい。
1） 頂点の座標を\( \ k \ \)を使って表しなさい。
2） \( \ 0 \leqq x \leqq 3 \ \) における最大値が\( \ 5 \ \)のとき、\( \ k \ \)の値を求めなさい。
3） (2)のときの放物線①を\( \ x \ \)軸方向に\( \ -1 \ \)、\( \ y \ \)軸方向に \( \ +1 \ \) 平行移動してできる放物線の方程式を求めなさい。
1） 頂点の座標を\( \ k \ \)を使って表しなさい。
2） \( \ 0 \leqq x \leqq 3 \ \) における最大値が\( \ 5 \ \)のとき、\( \ k \ \)の値を求めなさい。
3） (2)のときの放物線①を\( \ x \ \)軸方向に\( \ -1 \ \)、\( \ y \ \)軸方向に \( \ +1 \ \) 平行移動してできる放物線の方程式を求めなさい。
解法
平方完成して頂点を求める
$$\begin{align}&2x^2-4x+k \\\\ =&2\left( x^2-2x\right)+k \\\\ =&2\left( x-1\right)^2-2+k \end{align}$$ 頂点の座標は、\( \ \left( 1 \ , \ k-2\right) \ \)定義域と軸との位置関係
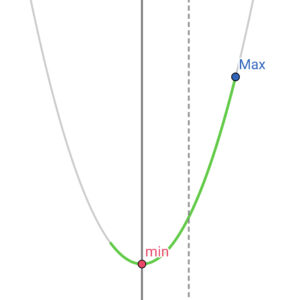最大値\( \ 5 \ \)をとるのは、\( \ x=3 \ \) のとき。$$\begin{align}2\left( 3-1\right)^2-2+k=&5 \\\\ 6+k=&5 \\\\ k=&-1 \end{align}$$
平行移動
（2)より①は、\( \ y=2\left( x-1\right)^2-3 \ \) であり、
頂点の座標は、\( \ \left( 1 \ , \ -3\right) \ \) である。
$$\begin{align}y=&2\left( x-1\color{red}{+1}\right)^2-3\color{red}{+1} \\\\ =&2x^2-2 \end{align}$$
ちなみに平行移動後の頂点の座標は
\( \ \left( 0 \ , \ -2\right) \ \)ですから、計算は正しいことになりますね。
放物線の平行移動の問題は、センター試験ではよく出ていましたし、共通テストでも引き継がれていると思います。
平行移動後の放物線の式から逆算するほうが楽なパターンなどもありますから、
おっくうがらずにどんどん練習してください。
\( \ \left( 0 \ , \ -2\right) \ \)ですから、計算は正しいことになりますね。
放物線の平行移動の問題は、センター試験ではよく出ていましたし、共通テストでも引き継がれていると思います。
平行移動後の放物線の式から逆算するほうが楽なパターンなどもありますから、
おっくうがらずにどんどん練習してください。
共有:
プロフィール
Author Profile