高校数学の「一次不等式の応用？」に関する問題を解いてみる。【Yahoo!知恵袋より】
読了時間: 約1分18秒
Yahoo!知恵袋の高校数学カテゴリに掲載されていた「一次不等式の応用？」に関する問題を解いてみました。
問題
太郎さんと次郎さんが合わせて\( \ 52 \ \)本のボールペンを持っている。いま、太郎さんが次郎さんに自分が持っているボールペンのちょうど\( \ \displaystyle\frac{1}{3} \ \)をあげてもまだ太郎さんの方が多く、さらに\( \ 3 \ \)本あげると次郎さんの方が多くなる。太郎さんが初めに持っていたボールペンの本数を求めよ。
解法
太郎さんが持っていたボールペンの本数を\( \ x \ \) とすると、次郎さんが持っていたボールペンの本数は \( \ 52-x \ \) である。
条件より以下の2つの不等式が表せる。
\begin{eqnarray} \left\{ \begin{array}{l} \displaystyle\frac{2}{3}x \gt 52-x+\displaystyle\frac{1}{3}x \ \cdots \ ① \\ \displaystyle\frac{2}{3}x-3 \lt 52-\displaystyle\frac{2}{3}x+3 \ \cdots \ ② \end{array} \right. \end{eqnarray} ①を整理して
\( \ x \gt 39 \ \)
②を整理して
\( \ x \lt 43.5 \ \)
①と②をまとめると
\( \ 39 \lt x \lt 43.5 \ \)
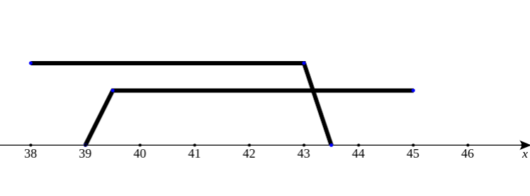
条件を満たす\( \ x \ \)は、
\( \ x=40, \ 41, \ 42, \ 43 \ \) である。
ただし、「持っているボールペンのちょうど\( \ \displaystyle\frac{1}{3} \ \)をあげ」たことから、
\( \ x \ \) は \( \ 3 \ \)の倍数である必要がある。
以上より、\( \ x=42 \ \)
こたえ
\( \ 42 \ \)本共有:
プロフィール
Author Profile
