中学数学の「列車−トンネル」問題（列車の長さがわからない）を解いてみる。(Yahoo!知恵袋より)

2021年6月17日2023年1月12日列車トンネル問題実用数学技能検定（数学検定数検),数検3級

読了時間: 約2分19秒

[mathjax]

問題

ある列車が、一定の速さで長さ$ \ 1440 \ $mのトンネルを通る時、列車全体がトンネルに隠れていたのは
$ \ 45 \ $秒間であった。また、この列車が同じ速さで長さ$ \ 240 \ $mの駅のホームを通過し始めてから通過し終わるまでに$ \ 15 \ $秒かかった。この列車の速さを求めなさい。

Contents

1. 列車の長さは？
2. トンネルの場合
3. ホーム通過の場合
4. まずは列車の長さを求めよう
5. あらためて列車の速度を求める
- 5.1. 共有:
- 5.2. 関連

列車の長さは？

「列車トンネル問題」でややこしいのは、トンネルや鉄橋、ホームなどを通過する列車そのものの長さも考えなければならないところです。
よくよく問題を読んでみると、トンネルの長さやホームの長さはわかっているのに、
列車の長さがわかっていません。
そこで、列車の長さを$ \ x\ $m として、列車の速さを求める式を立ててみます。

トンネルの場合

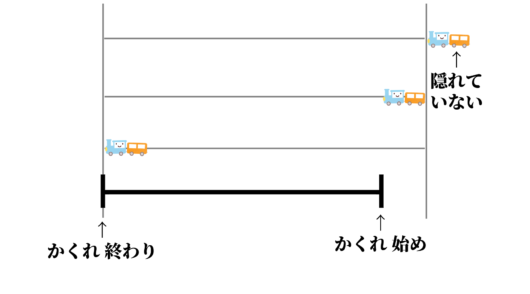灰色の線が、トンネルだと思ってください。
列車のイラストが三つありますが、
一番上の列車は、先端がトンネル入口に接しているので、「かくれてはいない」状態です。
ストップウォッチのボタンを押すのは、真ん中の列車の場合。
すなわち、列車の最後の車両がトンネル入り口と接したときです。
このとき、列車がトンネルに「完全にかくれ始めた」ことになります。
そして、「完全にかくれ始めた」とき列車の先端は、列車の長さぶん走っていることになりますね。
そして、「かくれ終わり」は、一番下の列車の場合。

「列車トンネル」問題は、列車先端の移動距離を考える問題でもあります。

つまり、列車先端は、トンネルの長さから列車の長さを引いた距離を進み、それにかかった時間が$ \ 45\ $秒ということになります。（図では、列車の移動距離を黒い太線で表しています）

ゆえに式は、
$ \ \ $$\Large \frac{1440-x}{45}$m/秒と表すことができます。

ホーム通過の場合

次に、ホーム通過時の式も立ててみましょう。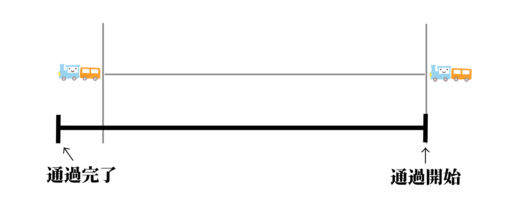

灰色の区間がホームだと考えてください。
列車先端が、ホームの右端に接したとき、ストップウォッチのボタンを押します。
そして、ホームの左端と列車の最後尾が接するとき、ストップウォッチを止めます。
そのとき、列車先端は、自分の長さぶん走っていることになりますね。
ゆえに式は、

$ \ \Large\frac{240+x}{15}\ $m/秒と表すことができます。

まずは列車の長さを求めよう

トンネルを通過したときも、ホームを通過したときも、
列車の速度は同じです。

式そのものは、速さを求めるものなのですが、
今回は列車の長さがわからないので、
まずはそれを求めてから、あらためて速度を求めていきます。

$ \ \Large\frac{1440-x}{45}=\frac{240+x}{15}\ $
$ \ 1440-x=3\left( 240+x\right)\ $
$ \ 4x=720\ $
$ \ x=180\ $
列車の長さは$ \ 180\ $mである。

あらためて列車の速度を求める

$ \ \Large\frac{1440-180}{45}\ $$ \ =28\ $
求める列車の速度は、$ \ 28\ $m/秒である。

Lukia

1秒で28mも進むとあれば、時速はどのぐらいだろう。と計算してみました。
$ \ \Large\frac{28\times 60\times 60}{1000} \ $$ \ =100.8\ $km/h
ホームに立ってたら、恐ろしい勢いでしょうね。

$$28 \ m/秒$$

関連

プロフィール

Author Profile

Lukia_74

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。

カテゴリー