「2通りで表されるベクトル」に関する問題を解いてみる。【たすきがけで比を統一せよ!!】

読了時間: 約7分37秒
Yahoo!知恵袋の高校数学カテゴリに掲載されていた「2通りで表されるベクトル」に関する問題を解いてみました。
問題
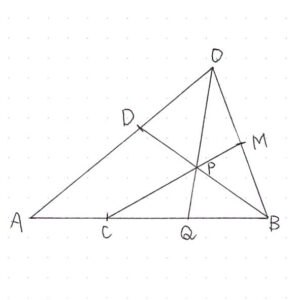
三角形 \( \ \triangle \mathrm{OAB} \ \) において、辺 \( \ \mathrm{OB} \ \) の中点を \( \ \mathrm{M} \ \) 、辺 \( \ \mathrm{AB} \ \) を \( \ 1:2 \ \) に内分する点を \( \ \mathrm{C} \ \) 、辺 \( \ \mathrm{OA} \ \) を \( \ 2:3 \ \) に内分する点を \( \ \mathrm{D} \ \) とする。また、2つの線分 \( \ \mathrm{CM} \ \) と \( \ \mathrm{BD} \ \) の交点を \( \ \mathrm{P} \ \) とし、直線 \( \ \mathrm{OP} \ \) と辺 \( \ \mathrm{AB} \ \) の交点を \( \ \mathrm{Q} \ \) とする。

(1) \( \ \overrightarrow{\mathrm{OM}} \ \), \( \ \overrightarrow{\mathrm{OD}} \ \), \( \ \overrightarrow{\mathrm{OC}} \ \) をそれぞれ \( \ \overrightarrow{\mathrm{OA}} \ \), \( \ \overrightarrow{\mathrm{OB}} \ \) を用いて表わせ。
(2) \( \ \overrightarrow{\mathrm{OP}} \ \) を \( \ \overrightarrow{\mathrm{OA}} \ \), \( \ \overrightarrow{\mathrm{OB}} \ \) を用いて表わせ。
(3) \( \ \overrightarrow{\mathrm{OQ}} \ \) を \( \ \overrightarrow{\mathrm{OA}} \ \), \( \ \overrightarrow{\mathrm{OB}} \ \) を用いて表わせ。
(1) \( \ \overrightarrow{\mathrm{OM}} \ \), \( \ \overrightarrow{\mathrm{OD}} \ \), \( \ \overrightarrow{\mathrm{OC}} \ \) をそれぞれ \( \ \overrightarrow{\mathrm{OA}} \ \), \( \ \overrightarrow{\mathrm{OB}} \ \) を用いて表わせ。
(2) \( \ \overrightarrow{\mathrm{OP}} \ \) を \( \ \overrightarrow{\mathrm{OA}} \ \), \( \ \overrightarrow{\mathrm{OB}} \ \) を用いて表わせ。
(3) \( \ \overrightarrow{\mathrm{OQ}} \ \) を \( \ \overrightarrow{\mathrm{OA}} \ \), \( \ \overrightarrow{\mathrm{OB}} \ \) を用いて表わせ。
解法
(1)
$$\begin{align}\overrightarrow{\mathrm{OM}}=&\displaystyle\frac{1}{2}\overrightarrow{\mathrm{OB}} \\\\ \overrightarrow{\mathrm{OD}}=&\displaystyle\frac{2}{5}\overrightarrow{\mathrm{OA}} \\\\ \overrightarrow{\mathrm{OC}}=&\displaystyle\frac{3}{5}\overrightarrow{\mathrm{OA}}+\displaystyle\frac{2}{5}\overrightarrow{\mathrm{OB}} \end{align}$$
(2)

\( \ \overrightarrow{\mathrm{OP}} \ \) は、\( \ \triangle \mathrm{ODB} \ \)において、線分 \( \ \mathrm{DB} \ \) を \( \ s:1-s \ \) に内分するから、
\( \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OD}}+\left( 1-s\right)\overrightarrow{\mathrm{OB}} \ \) である。
(ただし、\( \ s \ \) は \( \ 0 \lt s \lt 1 \ \) を満たす実数 )

同様に、\( \ \overrightarrow{\mathrm{OP}} \ \) は、\( \ \triangle \mathrm{OCM} \ \)において、線分 \( \ \mathrm{CM} \ \) を \( \ t:1-t \ \) に内分するから、
\( \ \overrightarrow{\mathrm{OP}}=t\overrightarrow{\mathrm{OC}}+\left( 1-t\right)\overrightarrow{\mathrm{OM}} \ \) である。
(ただし、\( \ t \ \) は \( \ 0 \lt t \lt 1 \ \) を満たす実数 )
ここで、\( \ \overrightarrow{\mathrm{DB}} \ \)と\( \ \overrightarrow{\mathrm{CM}} \ \)は一次独立であるから、
$$\begin{align}s\overrightarrow{\mathrm{OD}}+\left( 1-s\right)\overrightarrow{\mathrm{OB}}=&t\overrightarrow{\mathrm{OC}}+\left( 1-t\right)\overrightarrow{\mathrm{OM}} \\\\ \displaystyle\frac{2}{5}s\overrightarrow{\mathrm{OA}}+\left( 1-s\right)\overrightarrow{\mathrm{OB}}=&\displaystyle\frac{3}{5}t\overrightarrow{\mathrm{OA}}+\displaystyle\frac{2}{5}t\overrightarrow{\mathrm{OB}}+\left( 1-t\right)\cdot \displaystyle\frac{1}{2}\overrightarrow{\mathrm{OB}} \end{align}$$ 両辺を比較する。
$$\begin{align}\displaystyle\frac{2}{5}s=&\displaystyle\frac{3}{5}t \\\\ 2s=&3t \end{align}$$
$$\begin{align}1-s=&\displaystyle\frac{2}{5}t+\displaystyle\frac{1}{2}-\displaystyle\frac{t}{2} \\\\ 両辺&10倍して \\\\ 10-10s=&4t+5-5t\\\\ 5-10s=&-t\\\\ 5-5\cdot 2s=&-t\\\\ 5-5\cdot 3t=&-t\\\\ t=&\displaystyle\frac{5}{14}\end{align}$$ $$\begin{align}2s=&3t \\\\ s=&\displaystyle\frac{1}{2}\cdot \cdot 3\cdot t=\displaystyle\frac{3}{2}\cdot \displaystyle\frac{5}{14} \\\\ =&\displaystyle\frac{15}{28} \end{align}$$
$$\begin{align}\overrightarrow{\mathrm{OP}}=&\displaystyle\frac{2}{5}\cdot \displaystyle\frac{15}{28}\overrightarrow{\mathrm{OA}}+\displaystyle\frac{13}{28}\overrightarrow{\mathrm{OB}} \\\\ \\\\ \overrightarrow{\mathrm{OP}}=&\displaystyle\frac{3}{14}\overrightarrow{\mathrm{OA}}+\displaystyle\frac{13}{28}\overrightarrow{\mathrm{OB}} \end{align}$$
(3)
\( \ \overrightarrow{\mathrm{OQ}}=k\overrightarrow{\mathrm{OP}} \ \) とする。$$\begin{align}\overrightarrow{\mathrm{OM}}=&\displaystyle\frac{1}{2}\overrightarrow{\mathrm{OB}} \\\\ \overrightarrow{\mathrm{OD}}=&\displaystyle\frac{2}{5}\overrightarrow{\mathrm{OA}} \\\\ \overrightarrow{\mathrm{OC}}=&\displaystyle\frac{3}{5}\overrightarrow{\mathrm{OA}}+\displaystyle\frac{2}{5}\overrightarrow{\mathrm{OB}} \end{align}$$
(2)
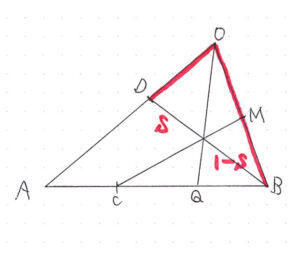
\( \ \overrightarrow{\mathrm{OP}} \ \) は、\( \ \triangle \mathrm{ODB} \ \)において、線分 \( \ \mathrm{DB} \ \) を \( \ s:1-s \ \) に内分するから、
\( \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OD}}+\left( 1-s\right)\overrightarrow{\mathrm{OB}} \ \) である。
(ただし、\( \ s \ \) は \( \ 0 \lt s \lt 1 \ \) を満たす実数 )
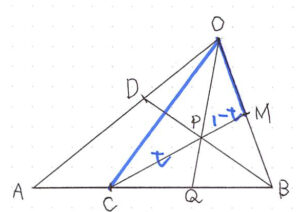
同様に、\( \ \overrightarrow{\mathrm{OP}} \ \) は、\( \ \triangle \mathrm{OCM} \ \)において、線分 \( \ \mathrm{CM} \ \) を \( \ t:1-t \ \) に内分するから、
\( \ \overrightarrow{\mathrm{OP}}=t\overrightarrow{\mathrm{OC}}+\left( 1-t\right)\overrightarrow{\mathrm{OM}} \ \) である。
(ただし、\( \ t \ \) は \( \ 0 \lt t \lt 1 \ \) を満たす実数 )
ここで、\( \ \overrightarrow{\mathrm{DB}} \ \)と\( \ \overrightarrow{\mathrm{CM}} \ \)は一次独立であるから、
$$\begin{align}s\overrightarrow{\mathrm{OD}}+\left( 1-s\right)\overrightarrow{\mathrm{OB}}=&t\overrightarrow{\mathrm{OC}}+\left( 1-t\right)\overrightarrow{\mathrm{OM}} \\\\ \displaystyle\frac{2}{5}s\overrightarrow{\mathrm{OA}}+\left( 1-s\right)\overrightarrow{\mathrm{OB}}=&\displaystyle\frac{3}{5}t\overrightarrow{\mathrm{OA}}+\displaystyle\frac{2}{5}t\overrightarrow{\mathrm{OB}}+\left( 1-t\right)\cdot \displaystyle\frac{1}{2}\overrightarrow{\mathrm{OB}} \end{align}$$ 両辺を比較する。
$$\begin{align}\displaystyle\frac{2}{5}s=&\displaystyle\frac{3}{5}t \\\\ 2s=&3t \end{align}$$
$$\begin{align}1-s=&\displaystyle\frac{2}{5}t+\displaystyle\frac{1}{2}-\displaystyle\frac{t}{2} \\\\ 両辺&10倍して \\\\ 10-10s=&4t+5-5t\\\\ 5-10s=&-t\\\\ 5-5\cdot 2s=&-t\\\\ 5-5\cdot 3t=&-t\\\\ t=&\displaystyle\frac{5}{14}\end{align}$$ $$\begin{align}2s=&3t \\\\ s=&\displaystyle\frac{1}{2}\cdot \cdot 3\cdot t=\displaystyle\frac{3}{2}\cdot \displaystyle\frac{5}{14} \\\\ =&\displaystyle\frac{15}{28} \end{align}$$
$$\begin{align}\overrightarrow{\mathrm{OP}}=&\displaystyle\frac{2}{5}\cdot \displaystyle\frac{15}{28}\overrightarrow{\mathrm{OA}}+\displaystyle\frac{13}{28}\overrightarrow{\mathrm{OB}} \\\\ \\\\ \overrightarrow{\mathrm{OP}}=&\displaystyle\frac{3}{14}\overrightarrow{\mathrm{OA}}+\displaystyle\frac{13}{28}\overrightarrow{\mathrm{OB}} \end{align}$$
(3)
(図より \( \ k \ \) は \( \ k \gt 1 \ \) を満たす実数)
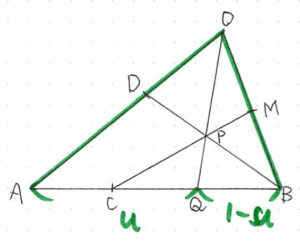
また、\( \ \overrightarrow{\mathrm{OQ}} \ \) は、\( \ \triangle \mathrm{OAB} \ \)において、線分 \( \ \mathrm{AB} \ \) を \( \ u:1-u \ \) に内分するから、
\( \ \overrightarrow{\mathrm{OQ}}=u\overrightarrow{\mathrm{OA}}+\left( 1-u\right)\overrightarrow{\mathrm{OB}} \ \) である。
(ただし、\( \ u \ \) は \( \ 0 \lt u \lt 1 \ \) を満たす実数 )
(2)より
\( \ \overrightarrow{\mathrm{OP}}=\displaystyle\frac{3}{14}\overrightarrow{\mathrm{OA}}+\displaystyle\frac{13}{28}\overrightarrow{\mathrm{OB}} \ \)だから、
$$\begin{align}u\overrightarrow{\mathrm{OA}}+\left( 1-u\right)\overrightarrow{\mathrm{OB}}=&\displaystyle\frac{3}{14}k\overrightarrow{\mathrm{OA}}+\displaystyle\frac{13}{28}k\overrightarrow{\mathrm{OB}}\quad より \\\\ u=&\displaystyle\frac{3}{14}k \\\\ これを&1-t=\displaystyle\frac{13}{28}k \ に代入する。\\\\ 1-\displaystyle\frac{3}{14}k=&\displaystyle\frac{13}{28}k\\\\ 28-6k=&13k\\\\ k=&\displaystyle\frac{28}{19} \quad \left( k \gt 1 \ を満たす\right) \end{align}$$ $$\overrightarrow{\mathrm{OQ}}=\displaystyle\frac{28}{19}\overrightarrow{\mathrm{OA}}-\displaystyle\frac{9}{19}\overrightarrow{\mathrm{OB}}$$
一次独立?

こういう内分の問題は、比を統一して解くようにしているのですが、
この問題は、どうにも比が統一できなかったので、ひとつのベクトルを2通りのやり方で表現して求めることになりました。
その際、必要になるのが「一次独立」のことわりです。
今も昔もこのあたりの知識がふわ〜っとしているので、私には説明できないのですが、
わかりやすく説明なさっているサイトがありましたので、御紹介しておきます。
この問題は、どうにも比が統一できなかったので、ひとつのベクトルを2通りのやり方で表現して求めることになりました。
その際、必要になるのが「一次独立」のことわりです。
今も昔もこのあたりの知識がふわ〜っとしているので、私には説明できないのですが、
わかりやすく説明なさっているサイトがありましたので、御紹介しておきます。

まとめると、
「\( \ \overrightarrow{\mathrm{OA}} \ \)と\( \ \overrightarrow{\mathrm{OB}} \ \)は一次独立である」 とは
同一平面上にある2つのベクトル\( \ \overrightarrow{\mathrm{OA}} \ \)と\( \ \overrightarrow{\mathrm{OB}} \ \)が
ともに\( \ \vec{0} \ \)でなく(ともに長さをもち)、
かつ 互いに平行でない関係にあることを指すようですね。
「\( \ \overrightarrow{\mathrm{OA}} \ \)と\( \ \overrightarrow{\mathrm{OB}} \ \)は一次独立である」 とは
同一平面上にある2つのベクトル\( \ \overrightarrow{\mathrm{OA}} \ \)と\( \ \overrightarrow{\mathrm{OB}} \ \)が
ともに\( \ \vec{0} \ \)でなく(ともに長さをもち)、
かつ 互いに平行でない関係にあることを指すようですね。
 以下の記事一覧に他のボリュームのブログカードを載せています。
以下の記事一覧に他のボリュームのブログカードを載せています。途中のボリュームからお読みになった方はこちらからどうぞ。
[subscribe2]











ディスカッション
コメント一覧
まだ、コメントがありません