【 10 / 12 】高校数学の「平面ベクトルの点Pの存在範囲」に関する問題を解いてみる。
読了時間: 約1分25秒
[mathjax]問題
\( \ \triangle \mathrm{OAB} \ \)について点\( \ \mathrm{P} \ \)が
\( \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}} \ \)
と \( \ -1 \leq s \leq 1 \ , \ -1 \leq t \leq 1 \ \)を満たしながら動くとき、
点\( \ \mathrm{P} \ \)の存在範囲を示せ。
（ ただし\( \ s \ \) , \( \ t \ \) はともに実数とする ）
\( \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}} \ \)
と \( \ -1 \leq s \leq 1 \ , \ -1 \leq t \leq 1 \ \)を満たしながら動くとき、
点\( \ \mathrm{P} \ \)の存在範囲を示せ。
（ ただし\( \ s \ \) , \( \ t \ \) はともに実数とする ）
解法
\( \ \triangle \mathrm{OAB} \ \)が\( \ xy \ \)平面上ならぬ\( \ st \ \)平面上にあるとし、グラフを描いて領域の問題として考えていきましょう。
\( \ \vert \overrightarrow{\mathrm{OA}} \vert=1 \ \) （\( \ s=1 \ \)）、
\( \ \vert \overrightarrow{\mathrm{OB}} \vert=1 \ \) （\( \ t=1 \ \)）とします。
\( \ st \ \)平面上に2つの領域\( \ -1 \leq s \leq 1 \ \)と\( \ -1 \leq t \leq 1 \ \)を描きます。
求める領域は、四角形\( \ \mathrm{CDEF} \ \)の周上とその内部となります。
よって、こたえは「 四角形\( \ \mathrm{CDEF} \ \)の周上とその内部 」となります。
\( \ \vert \overrightarrow{\mathrm{OA}} \vert=1 \ \) （\( \ s=1 \ \)）、
\( \ \vert \overrightarrow{\mathrm{OB}} \vert=1 \ \) （\( \ t=1 \ \)）とします。
\( \ st \ \)平面上に2つの領域\( \ -1 \leq s \leq 1 \ \)と\( \ -1 \leq t \leq 1 \ \)を描きます。
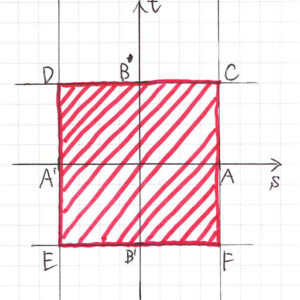
求める領域は、四角形\( \ \mathrm{CDEF} \ \)の周上とその内部となります。
よって、こたえは「 四角形\( \ \mathrm{CDEF} \ \)の周上とその内部 」となります。
ベクトルと考えるから難しいのであって、 \( \ s \ \)と\( \ t \ \)に関する領域の問題。と考えればよいのではないかな。と思っています。
式変形はできたほうがいいに決まっていますが、この領域の問題。という考え方を確かめる術にしながら、式変形の練習をしていくのが習得の近道になるかも。
式変形はできたほうがいいに決まっていますが、この領域の問題。という考え方を確かめる術にしながら、式変形の練習をしていくのが習得の近道になるかも。
こたえ
四角形\( \ \mathrm{CDEF} \ \)の周上とその内部
共有:
プロフィール
Author Profile
