中学数学の2種類の濃度の食塩水を混ぜる問題(その9)

読了時間: 約5分52秒
[mathjax]

Lukia
2種類の濃度の食塩水を混ぜ合わせる問題も、一応今回が最後となります。
次回からはまた別のパターンの問題を解いていきます。
仕上げがてら、問題を解いてみてくださいね。
それでは、さっそく問題を載せてみます。
いったんスクロールの手を止めて、解いてみてください。
次回からはまた別のパターンの問題を解いていきます。
仕上げがてら、問題を解いてみてくださいね。
それでは、さっそく問題を載せてみます。
いったんスクロールの手を止めて、解いてみてください。
問題




もも
問題文を読んでみると、6行目に「また、」とありますから、ふたつに分けられそうですね。
ということは、まず、前半となる5行目までの表を描いてみようかな。
ということは、まず、前半となる5行目までの表を描いてみようかな。
問題文前半(5行目まで)
表に書き込む。

もも
横長の線を3本と、その線を4等分するように縦の線を3本引いていきます。

Lukia
ももちゃんは、以下のような表を描いています。
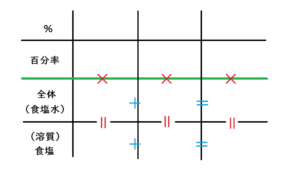

もも
では、前半を見ながら、表に数字を書き込んでいこう。


もも
今回、食塩水にはA、Bと名前がついているんですね。
では、表だと左から2番目の列を食塩水Aとして、
左から3番目の列を食塩水Bとします。
では、表だと左から2番目の列を食塩水Aとして、
左から3番目の列を食塩水Bとします。

もも
あれっ、今回は、①と③は埋まらないんですね。

Lukia
そうですね。問題文後半の最後の2行を読んでもらえばわかりますが、
食塩水Aと食塩水Bのそれぞれの濃度を求める問題なので、
①と③には具体的な数があてられてないんですね。
食塩水Aと食塩水Bのそれぞれの濃度を求める問題なので、
①と③には具体的な数があてられてないんですね。

もも
ふ~ん。そうかぁ。
じゃ、Aを \(\Large x\) 、Bを \(\Large y\) としてもいいですか?
じゃ、Aを \(\Large x\) 、Bを \(\Large y\) としてもいいですか?

Lukia
いいですよ。

もも
では、①が \(\Large x\) 、
②が \(\Large y\) となります。
あとは、わりと簡単かな。
まず、⑤は6、
②は 200、
④は 300です。
「全体の重さ」の段の「横はたし算」はここでやってしまってもかまわないので、
②+④=⑥ より、
⑥は 500 ということになります。
②が \(\Large y\) となります。
あとは、わりと簡単かな。
まず、⑤は6、
②は 200、
④は 300です。
「全体の重さ」の段の「横はたし算」はここでやってしまってもかまわないので、
②+④=⑥ より、
⑥は 500 ということになります。
%を百分率に直しておく。

もも
百分率に直すのは簡単。
左から、 \(\Large \frac{x}{100}\) ・ \(\Large \frac{y}{100}\) ・\(\Large \frac{6}{100}\) となります。
左から、 \(\Large \frac{x}{100}\) ・ \(\Large \frac{y}{100}\) ・\(\Large \frac{6}{100}\) となります。
縦はかけ算・横はたし算

もも
次は、縦の列だな。
「縦はかけ算」をして、表の一番下の段のマスをうめていきます。
食塩水Aの列は、\(\Large \frac{x}{100}\times 200\) 、
食塩水Bの列は、\(\Large \frac{y}{100}\times 300\) 、
さらに6%の食塩水は、\(\Large \frac{6}{100}\times 500\) となります。
「縦はかけ算」をして、表の一番下の段のマスをうめていきます。
食塩水Aの列は、\(\Large \frac{x}{100}\times 200\) 、
食塩水Bの列は、\(\Large \frac{y}{100}\times 300\) 、
さらに6%の食塩水は、\(\Large \frac{6}{100}\times 500\) となります。
一番下の段の「たし算」をする。

もも
表の一番下の段のマスがすべてうまったので、
あとは、「横はたし算」をして、式を立てていきます。
式は、
\(\Large \frac{x}{100}\times 200+\frac{y}{100}\times 300=\frac{6}{100}\times 500\) となります。
あとは、「横はたし算」をして、式を立てていきます。
式は、
\(\Large \frac{x}{100}\times 200+\frac{y}{100}\times 300=\frac{6}{100}\times 500\) となります。

もも
前半はわりと簡単だったな~。

もも
あれっ、Lukia先生?
なんで、いじけてるんですか?
なんで、いじけてるんですか?

Lukia
かなり前半で、ももちゃんにおいていかれまして・・・(涙)

もも
んもぉ~、次行きますよっ♪
問題文後半(6行目から)

Lukia
ブログの特性上、問題文を見るには、かなり上のほうまで戻らなければならないので、
問題文の後半部分だけを表示してみましょうね。
問題文の後半部分だけを表示してみましょうね。

表に書き込む。

Lukia
では、再度、以下のような表を描いて、数字を書き込んでいきましょう。
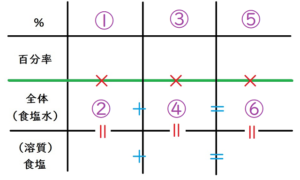

もも
前半で、
①は 、
③は と決めましたから、それぞれ書き込んで・・・。
⑤は 7 です。
そして、②が 300 、
④が 200 ですね。
ということは、⑥は 500 ですね。
①は 、
③は と決めましたから、それぞれ書き込んで・・・。
⑤は 7 です。
そして、②が 300 、
④が 200 ですね。
ということは、⑥は 500 ですね。

Lukia
表を描くことで、前半と後半の共通点やちがいなどがよくわかりますね。
それでは、次に進みましょう。
それでは、次に進みましょう。
%を百分率に直しておく。

もも
①、③、⑤を百分率に直します。
左から、 \(\Large \frac{x}{100}\) ・ \(\Large \frac{y}{100}\) ・ \(\Large \frac{7}{100}\) となりますね。
左から、 \(\Large \frac{x}{100}\) ・ \(\Large \frac{y}{100}\) ・ \(\Large \frac{7}{100}\) となりますね。
縦はかけ算・横はたし算

もも
前半の表と同じく、「縦はかけ算」をして、
表の一番下の段のマスを埋めていきます。
表の一番下の段のマスを埋めていきます。

Lukia
左から、\(\Large \frac{x}{100}\times 300 ・ \frac{y}{100}\times 200 ・ \frac{7}{100}\times 500\) となりますっ♪

もも
大人げないなぁ、もぉ・・・。
一番下の段の「たし算」をする。

Lukia
あとは、「横はたし算」をすることで、式を立てられますね。

もも
言っていいんですか?

Lukia
はい。さっきので、満足しましたから。

もも
そうなんだ・・・。
では、後半部分の式は、
\(\Large \frac{x}{100}\times 300+\frac{y}{100}\times 200=\frac{7}{100}\times 500\) となります。
では、後半部分の式は、
\(\Large \frac{x}{100}\times 300+\frac{y}{100}\times 200=\frac{7}{100}\times 500\) となります。
連立方程式を解く。

Lukia
この問題では、食塩水Aと食塩水Bの濃度がわからないため、
それぞれ、\(\Large x\) ・ \(\Large y\) とおきました。
おいた文字の数だけ、式を立てる必要がありますから、前半と後半にわけて表を描き、ふたつの式を立てたわけですね。
それぞれ、\(\Large x\) ・ \(\Large y\) とおきました。
おいた文字の数だけ、式を立てる必要がありますから、前半と後半にわけて表を描き、ふたつの式を立てたわけですね。

もも
そうでした。

Lukia
前半の式を①、
後半の式を②とすると、
以下のようになりますね。
後半の式を②とすると、
以下のようになりますね。
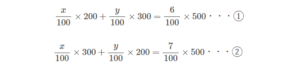

Lukia
どちらの式にも、両辺に分母の100があり、
分子にも100があることになりますから、
式はもっと簡単な形になりますね。
分子にも100があることになりますから、
式はもっと簡単な形になりますね。
![]()

Lukia
ふたつの式そのものは、たし算をすると考えてください。
つまり、式①+式②という操作をおこないます。
つまり、式①+式②という操作をおこないます。

もも
はい。

Lukia
小学校で筆算をやったと思いますが、
ぱっと見、筆算してみるとどうですか?
ぱっと見、筆算してみるとどうですか?

もも
\(\Large 5x+5y=13\times 5\) になります。

Lukia
高校数学ならば、この式も解けるようになるのですが、
中学数学レベルでは解けません。
というわけで、それぞれを求めるために、まずは\(\Large x\) か \(\Large y\) のどちらかを消したいのですが、
ももちゃん、どっちがいいですか?
中学数学レベルでは解けません。
というわけで、それぞれを求めるために、まずは\(\Large x\) か \(\Large y\) のどちらかを消したいのですが、
ももちゃん、どっちがいいですか?

もも
まぁ、\(\Large y\) ですかねぇ。

Lukia
わかりました。
では、式①と式②の を見てもらうと、
それぞれ、\(\Large 3y\) と \(\Large 2y\) となっていますね。
最小公倍数はいくつですか?
では、式①と式②の を見てもらうと、
それぞれ、\(\Large 3y\) と \(\Large 2y\) となっていますね。
最小公倍数はいくつですか?

もも
\(\Large 6y\) です。

Lukia
はい。それでは、その最小公倍数になるためには、
式①と、式②には、それぞれいくつをかけたらいいですか?
式①と、式②には、それぞれいくつをかけたらいいですか?

もも
ええっと・・・
式①は、\(\Large 3y\) だったから、
\(\Large 6y\) になるためには、\(\Large 2\) をかけなくてはいけませんね。
式①は、\(\Large 3y\) だったから、
\(\Large 6y\) になるためには、\(\Large 2\) をかけなくてはいけませんね。

Lukia
そうですね。では、式②のほうは?

もも
ええっと・・・
\(\Large 2y\) でしたから、
\(\Large 6y\) になるためには、\(\Large 3\) をかけます。
\(\Large 2y\) でしたから、
\(\Large 6y\) になるためには、\(\Large 3\) をかけます。

Lukia
そうですね。
そして、それぞれの式をもう一度見てほしいのですが、
\(\Large y\) の項は、どちらも+(プラス)でつながれているんですよね。
そして、それぞれの式をもう一度見てほしいのですが、
\(\Large y\) の項は、どちらも+(プラス)でつながれているんですよね。

もも
ふむふむ。

Lukia
ふたつの式そのものはたし算をするのですが、
今回、\(\Large y\) は「プラス」でつながれているので、
「消える」すなわち、「0(ゼロ)」になりませんでした。
今回、\(\Large y\) は「プラス」でつながれているので、
「消える」すなわち、「0(ゼロ)」になりませんでした。

もも
でも、\(\Large y\) を消したいんだから、
片方が「マイナス」だったらいいのになぁ・・・。
片方が「マイナス」だったらいいのになぁ・・・。

Lukia
おろっ!ももちゃん、いいこといいますね!
そうです、片方を「マイナス〇(〇は数字)」にしてかければいいんです。
そうです、片方を「マイナス〇(〇は数字)」にしてかければいいんです。

もも
そうなんですね!
じゃ、②の式に \(\Large 3\) をかけるんだったけど、
\(\Large -3\) にしてかけてみようかな。
じゃ、②の式に \(\Large 3\) をかけるんだったけど、
\(\Large -3\) にしてかけてみようかな。

Lukia
ということは、
①×2+②×(-3)となりますね。
①×2+②×(-3)となりますね。
![]()

Lukia
それぞれ展開して、筆算の形にしてみましょう。
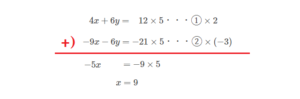

Lukia
\(\Large x=9\) を式①または式②に代入して \(\Large y\) を求めます。
今回は、式①に代入しましょうか。
今回は、式①に代入しましょうか。
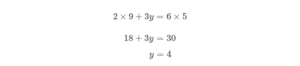

Lukia
以上より、\(\Large x=9\) 、\(\Large y=4\) とわかりましたので、
食塩水Aの濃度は、9%
食塩水Bの濃度は、4%とわかりました。
食塩水Aの濃度は、9%
食塩水Bの濃度は、4%とわかりました。
おわりに
連立方程式の解き方を少していねいにやったので、文字数も3500字近くになってしまいました。
読むのが大変だったかもしれませんね。
さて、一応今回で、「2種類の濃度の食塩水を混ぜ合わせる」問題は終了となります。
また、おもしろそうな問題があれば、その10があるかもしれません。
それでは、再度、問題と答えを載せておわりにしましょう。



[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません