中学数学の2種類の濃度の食塩水を混ぜる問題(その6)

読了時間: 約4分3秒
[mathjax]

Lukia
二種類の食塩水を混ぜる問題も、はや6問めとなりました。
どうですか。だいぶん慣れてきましたか?
今回ぐらいから、少しずつ複雑な問題になりますよ。
それでは、問題を載せますので、少しの間スクロールの手を止めて解いてみてください。
どうですか。だいぶん慣れてきましたか?
今回ぐらいから、少しずつ複雑な問題になりますよ。
それでは、問題を載せますので、少しの間スクロールの手を止めて解いてみてください。
問題
質量パーセント濃度が16%の食塩水と8%の食塩水を混ぜて、ある濃度の食塩水を作ろうとしたところ、
分量を逆にしたため、濃度が11%の食塩水400gができてしまった。
本来作ろうとした食塩水の濃度は何%であったか。
分量を逆にしたため、濃度が11%の食塩水400gができてしまった。
本来作ろうとした食塩水の濃度は何%であったか。

もも
中学校の数学もだし、小学校の算数のときもそうですが、
文章題に出てくる人は、たいていうっかりしてますよね。
なんで、間違えるかなぁ、もう!(怒)って思っちゃいます。
文章題に出てくる人は、たいていうっかりしてますよね。
なんで、間違えるかなぁ、もう!(怒)って思っちゃいます。

Lukia
いや、考えごとしてると、うっかり間違えたりするもんですよ。(汗)

もも
まったくもぉ、うっかりにもほどがありますよ。(ぶつぶつ・・・。)
表に書き込む。

Lukia
そ、それでは、表を描いてみましょうねっ。(汗)

もも
なにか、思い当たるフシがあるんですね?
ま、聞かないでおいてあげましょう。( ̄ー ̄)ニヤリッ
じゃ、いつもどおり、横長の線を3本と、線の幅を四等分するように縦の線を3本引きます。
ま、聞かないでおいてあげましょう。( ̄ー ̄)ニヤリッ
じゃ、いつもどおり、横長の線を3本と、線の幅を四等分するように縦の線を3本引きます。

Lukia
ももちゃんは、以下のような表を描いていますよ~。
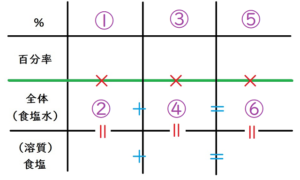

もも
そして、問題を読みながら、わかる数字を書き込んでいく。と。
今回は、食塩水の濃度がみっつわかってて、二種類の食塩水を混ぜてできた食塩水が400gってことだから、
①が16、
③が8、
⑤が11、
⑥が400 とわかります。
今回は、食塩水の濃度がみっつわかってて、二種類の食塩水を混ぜてできた食塩水が400gってことだから、
①が16、
③が8、
⑤が11、
⑥が400 とわかります。

Lukia
できあがった食塩水の重さがわかっているあたりは、前回やった問題とちょっと似ていますね。

もも
そうですね。
ひとまず、①を \(\Large x\) とおいて。
ひとまず、①を \(\Large x\) とおいて。

もも
全体の重さの段の「横はたし算」をここでやってしまったほうが楽そうだなぁ。
・・・。ということは、
②+④=⑥だから、
④は、\(\Large 400-x\) ということになりますね。
・・・。ということは、
②+④=⑥だから、
④は、\(\Large 400-x\) ということになりますね。

Lukia
では、次に進みましょう。
%を百分率に直しておく。

もも
%を百分率に直すのは、簡単。
左から、 \(\Large \frac{16}{100} ・ \frac{8}{100} ・ \frac{11}{100}\)
左から、 \(\Large \frac{16}{100} ・ \frac{8}{100} ・ \frac{11}{100}\)
となりますね。
縦はかけ算・横はたし算

Lukia
表の①から⑥と、百分率がすべてうまったので、
縦のかけ算をしていきます。
縦のかけ算をしていきます。

もも
はい。
16%の食塩水は、 \(\Large \frac{16}{100}\times x\)
8%の食塩水は、 \(\Large \frac{8}{100}\times \left( 400-x\right)\)
11%の食塩水は、 \(\Large \frac{11}{100}\times 400\)
16%の食塩水は、 \(\Large \frac{16}{100}\times x\)
8%の食塩水は、 \(\Large \frac{8}{100}\times \left( 400-x\right)\)
11%の食塩水は、 \(\Large \frac{11}{100}\times 400\)
となります。

Lukia
ももちゃん、それでは次をお願いします。
一番下の段の「たし算」をする。

もも
は~い。
「縦はかけ算」をして、表の一番下の段がうまりました。
「横はたし算」というルールなので、一番下の段のたし算をして、式を立てます。
「縦はかけ算」をして、表の一番下の段がうまりました。
「横はたし算」というルールなので、一番下の段のたし算をして、式を立てます。

もも
\(\Large \frac{16}{100}\times x+ \frac{8}{100}\times \left( 400-x\right) = \frac{11}{100}\times 400\)
となりますよね。
これを計算すると、\(\Large x = 150\) だから、
16%の食塩水は、 \(\Large 150g\) で、
8%の食塩水は、 \(\Large 250g\) ・・・。

もも
あれっ、答えるのは、それぞれ混ぜ合わせた食塩水の重さじゃない!(汗)

Lukia
そうなんです。表を描き、計算をしていく間にうっかり忘れていますが、
間違って混ぜ合わせた食塩水の重さを求めただけで、
「本来できるはずの食塩水の濃度」を答えなければならないんですよね。
間違って混ぜ合わせた食塩水の重さを求めただけで、
「本来できるはずの食塩水の濃度」を答えなければならないんですよね。

もも
じゃ、もう一回、表を描かないといけないってことか。
本来作ろうとした食塩水の濃度を求める。


もも
あらためて、表を描いて、数字を書き込んでみます。
①と③と⑤は、これまでに使っていた数字をそのまま書き込めばいいとして・・・。
150gと250gを間違えて、逆に入れてしまったわけだから、
②が250g、④が150gということになりますね。
①と③と⑤は、これまでに使っていた数字をそのまま書き込めばいいとして・・・。
150gと250gを間違えて、逆に入れてしまったわけだから、
②が250g、④が150gということになりますね。

Lukia
そうですね。そして、あらためて求めるのは、「本来作ろうとした食塩水の濃度」です。
\(\Large x\) としたいところですが、すでに使っているので、
別の文字を使い、 \(\Large y\) とおいてやりましょう。
ここさえ補えれば、もう百分率は直してありますし、一気に一番下の段の式を立てられますね。
\(\Large x\) としたいところですが、すでに使っているので、
別の文字を使い、 \(\Large y\) とおいてやりましょう。
ここさえ補えれば、もう百分率は直してありますし、一気に一番下の段の式を立てられますね。

もも
じゃ、一応「本来作ろうとした食塩水の濃度を \(\Large y\) とおく。」とことわっといて・・・。
\(\Large \frac{16}{100}\times 250 + \frac{8}{100}\times150 = \frac{y}{100}\times 400\)か。
\(\Large \frac{16}{100}\times 250 + \frac{8}{100}\times150 = \frac{y}{100}\times 400\)か。

もも
\(\Large y=13\) だから、
「本来作ろうとした食塩水の濃度」は、 \(\Large 13%\) です。
「本来作ろうとした食塩水の濃度」は、 \(\Large 13%\) です。

Lukia
そのとおり!
連立方程式で計算することもできる?


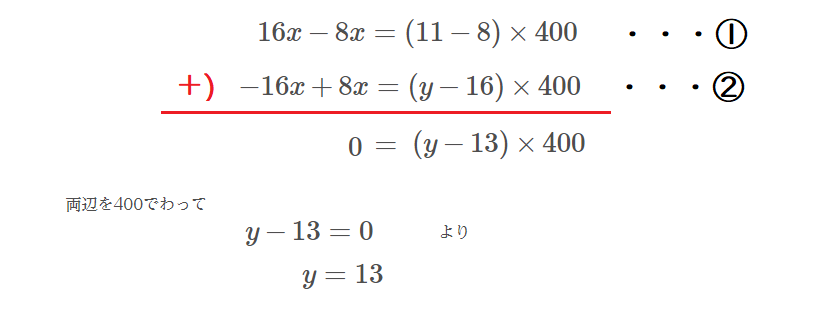


もも
なるほど、「連立方程式」を習ったなら、
そうやって解けないかどうかを考えてみるといいんですね。
ちょっと難しいことを習うんだから、答えが手間なく求められなくちゃ
お得感がないですよね。
そうやって解けないかどうかを考えてみるといいんですね。
ちょっと難しいことを習うんだから、答えが手間なく求められなくちゃ
お得感がないですよね。

Lukia
「お得感」って。(笑)
こたえ
13%
[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません