中学数学の2種類の濃度の食塩水を混ぜる問題(その3)

読了時間: 約3分26秒
[mathjax]

Lukia
今回も、2種類の濃度の食塩水を混ぜ合わせる問題です。

もも
表を書いて、手順を守れば解けたので、練習したかったところです。

Lukia
それでは、さっそく問題をお見せしましょうね。
いったんスクロールを止めて、解いてから答え合わせをしていくとよいかもしれません。
いったんスクロールを止めて、解いてから答え合わせをしていくとよいかもしれません。
問題
濃度8%の食塩水100gに、濃度15%の食塩水を混ぜ合わせたら、濃度10%の食塩水ができた。
このとき、濃度15%の食塩水は何g混ぜたか。
このとき、濃度15%の食塩水は何g混ぜたか。
表に書き込む。

もも
今回も、数字は4つですね。
じゃ、前回に引き続き、表を描いていきます。
じゃ、前回に引き続き、表を描いていきます。

Lukia
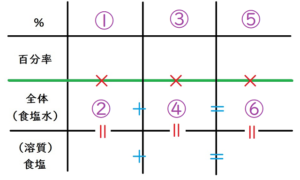
はい。このページを初めて見る方のために、簡易の表を示しておきましょうね。
ももちゃんは、この表に書き込んで、食塩水の問題を解いていきます。
ももちゃんは、この表に書き込んで、食塩水の問題を解いていきます。

もも
8%の食塩水が100gあるから、
①に8、
②に100 を書き込みます。
①に8、
②に100 を書き込みます。

Lukia
♪

もも
次に、15%の食塩水があるから、
③に15 を書き込んで・・・。
重さは書いてないから、ひとまず飛ばそうっと。
③に15 を書き込んで・・・。
重さは書いてないから、ひとまず飛ばそうっと。

Lukia
そうですね。わかっていることから確実にうめていきましょう。

もも
はい。
そして、できあがったのが10%の食塩水か。
じゃ、⑤に10 を書き込めばいいのですか?
そして、できあがったのが10%の食塩水か。
じゃ、⑤に10 を書き込めばいいのですか?

Lukia
はい。そのとおりです。
さて、番号は①から⑥までふってあるのに、⑤と⑥がうまりませんでしたね。
どちらのせいですか?
さて、番号は①から⑥までふってあるのに、⑤と⑥がうまりませんでしたね。
どちらのせいですか?

もも
こういうときは、問題文にもどったほうがいいよね・・・。
「15%の食塩水は何g混ぜたか。」とあるから、
15%の食塩水の重さを表す、⑤を書いてないせいかな?
「15%の食塩水は何g混ぜたか。」とあるから、
15%の食塩水の重さを表す、⑤を書いてないせいかな?

Lukia
そうですね。
ですから、15%の食塩水の重さを \(\Large x\) としてみましょう。
ですから、15%の食塩水の重さを \(\Large x\) としてみましょう。

もも
はい。
%を百分率に直しておく。

もも
%を百分率に直しておこうっと。

Lukia
ここは、慣れてきたら省いてもいいのですが、
試験で式も解答しなければならないとき、%は百分率に直す必要がありますからね。
確認がてら、表に書き込んでおきましょう。
試験で式も解答しなければならないとき、%は百分率に直す必要がありますからね。
確認がてら、表に書き込んでおきましょう。

もも
はい。一気にいっちゃいますよ。
左から、
$$\Large\frac{8}{100} ・ \frac{15}{100} ・ \frac{10}{100}$$
左から、
$$\Large\frac{8}{100} ・ \frac{15}{100} ・ \frac{10}{100}$$
です♪
縦はかけ算・横はたし算

Lukia
それでは、「縦はかけ算・横はたし算」に入っていきましょう。
ちなみに、場合によっては、「横はたし算・縦はかけ算」の順でやったほうがいいこともあります。
操作自体をまちがわなければ、順番にこだわる必要はありません。
ちなみに、場合によっては、「横はたし算・縦はかけ算」の順でやったほうがいいこともあります。
操作自体をまちがわなければ、順番にこだわる必要はありません。

もも
そういえば、⑥がまだうまってないから、
かけ算はできませんよね。
ということは、重さの段のたし算を先にやっちゃえばいいのか。
かけ算はできませんよね。
ということは、重さの段のたし算を先にやっちゃえばいいのか。

Lukia
そのとおり。

もも
\(\Large 100+x\) だから、
⑥には、
$$\Large \left( 100+x\right)$$
⑥には、
$$\Large \left( 100+x\right)$$
が入ります。

Lukia
そうですね。
それでは、縦の列をかけ算して、一番下の段のマスにうめていきましょう。
全部ももちゃんにやらせても悪いので、8%の食塩水は
私がやろうかな。
それでは、縦の列をかけ算して、一番下の段のマスにうめていきましょう。
全部ももちゃんにやらせても悪いので、8%の食塩水は
私がやろうかな。

もも
出番が少なくてくやしいんでしょ~。(笑)

Lukia
うぐぁぐぁ・・・。
そ、そんなことはありませんッ。
えっと、8%の食塩水が100gですから、
$$\Large\frac{8}{100}\times 100$$
そ、そんなことはありませんッ。
えっと、8%の食塩水が100gですから、
$$\Large\frac{8}{100}\times 100$$
となりますねっ。

もも
じゃ、15%の食塩水と、10%の食塩水は、ももがやろうっと。
まず、15%の食塩水は、
$$\Large\frac{15}{100}\times x$$
まず、15%の食塩水は、
$$\Large\frac{15}{100}\times x$$
です。

もも
そして、10%の食塩水は、
$$\Large\frac{10}{100}\times\left( 100+x\right)$$
$$\Large\frac{10}{100}\times\left( 100+x\right)$$
となります。
一番下の段の「たし算」をする。

Lukia
縦の列をかけ算したことによって、一番下の段のマスがうまりました。
「横はたし算」をして、式を立てます。
「横はたし算」をして、式を立てます。

もも
は~い。
$$\Large\frac{8}{100}\times 100 + \frac{15}{100}\times x =\frac{10}{100}\times\left( 100+x\right)$$
$$\Large\frac{8}{100}\times 100 + \frac{15}{100}\times x =\frac{10}{100}\times\left( 100+x\right)$$
です♪

Lukia
式が立てられたので、あとは計算するだけですね。
計算していくと、
\(\Large x = 40\) となり、
\(\Large 40g\)が正解となります。
計算していくと、
\(\Large x = 40\) となり、
\(\Large 40g\)が正解となります。
おわりに

Lukia
いかがでしたか?
だいぶん食塩水の問題にも慣れてきたと思います。
この調子でがんばっていきましょうね。
だいぶん食塩水の問題にも慣れてきたと思います。
この調子でがんばっていきましょうね。
こたえ
40g[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません