中学数学の食塩水の融合問題（その1）

2018年7月8日2023年1月15日食塩水の濃度実用数学技能検定（数学検定数検),数検3級

読了時間: 約3分24秒

Lukia

これまでは、ある濃度の食塩水に、「別の濃度の食塩水」や「食塩」、「水」がそれぞれ加えられる問題を解いてきました。
しかし、今回は、さらにもう一つ別のものを加えるという、融合問題です。
現在は、縦と横3本ずつの線を引いて、表を描いていますが、
今回は、どちらかにもう1本線を加えれば、いつもどおり式が立てられます。
それでは、以下に問題を示しますので、上のヒントをもとに表を作成し、解いてみてください。

[mathjax]

問題

ある濃度の食塩水500gに水100gを加え、さらに質量パーセント濃度が6%の食塩水200gを加えたところ、4％の食塩水になった。
はじめの食塩水の濃度は何％であったか。

表に書き込む。

もも

表を描きたいけれど、Lukia先生のヒントによると、縦か横のどっちかに1本線が増えるんですよね。

Lukia

そうですね。どっちでしょう♪

もも

問題文から、「どんな操作をしたのか。」ということだけを抜き出してみると、
食塩水に水を加えて、さらに別の食塩水を加えた。とわかります。

もも

数式みたいに表すと、
食塩水 + 水 + 食塩水＝食塩水　となるから・・・
増やすのは縦線です！

Lukia

その通りです。
よくわかりましたね。
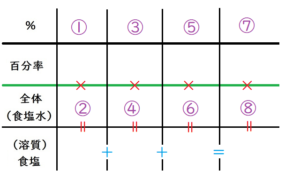
というわけで、今回は、横長の線を3本を引き、
それを5等分するように、4本の縦の線を引いて、表を描きます。
以下のような表になりますね。

Lukia

いつもは6つのマスを埋めますが、今回は、８つありますので、注意してくださいね。

もも

とはいえ、やることはいっしょだからなぁ。
さっそくですが、①は、「ある濃度」とあるし、問題文の最後にも、
「はじめの食塩水の濃度は何％か」とあるので、
①を $\Large x$ とします。

Lukia

問題文全体に目がやれるようになっているんですね。
たいしたものです。

もも

てへっ。
①は $\Large x$ で、その重さが500ｇだから、
②は500です。

もも

次に水、つまり「0％食塩水」を加えているので、
③は0、
④は100です。

Lukia

質量パーセント濃度とは、これまで扱ってきた「濃度」のことです。
実は、この問題、高校化学の問題なんですね。

もも

そうなんだ。
じゃ、⑤は6で、
⑥は200となります。

もも

いつもと同じように、「全体の重さの段」は「横はたし算」ができますから、
②+④+⑥=⑧となりますので、
$\Large 500+100+200=800$ となり、
⑧は800 とあらわせます。

％を百分率に直しておく。

Lukia

では、%を百分率に直してください。

もも

はい。
左から、
$\Large \frac{x}{100}$ ・ $\Large \frac{0}{100}$ ・ $\Large \frac{6}{100}$ ・ $\Large \frac{4}{100}$ です。

縦はかけ算・横はたし算

Lukia

それでは、表の一番下の段のマスをうめるために、
縦の列について、「縦はかけ算」をしていきましょう。

もも

はい。
まず、①の列は、
$\Large \frac{x}{100}\times 500$ となります。

Lukia

次に、③の列ですが、水の列ですから、
計算するまでもなく、$\Large 0$ となりますね。

もも

はい。
さらに加えた⑤の食塩水の列は、
$\Large \frac{6}{100}\times 200$ となります。

もも

そしてできあがりの食塩水を表す⑦の列は、
$\Large \frac{4}{100}\times 800$ となります。

一番下の段の「たし算」をする。

Lukia

表の一番下の段のマスがすべて埋まりましたので、
式が立てられますね。

もも

はい。
$\Large \frac{x}{100}\times 500+\frac{6}{100}\times 200=\frac{4}{100}\times 800$ となります。

Lukia

では、計算をしていきましょう。

$$\Large \frac{x}{100}\times 500+\frac{6}{100}\times 200=\frac{4}{100}\times 800$$
両辺の分母の100をはらって、両辺を100でわると、
$$\Large 5x+6\times 2=4\times 8$$
$$\Large 5x=32-12=20$$
$$\Large x=4$$

もも

はじめの食塩水の濃度は、4％　でした。