中学数学の食塩水に「水」を混ぜる問題（その3）

2018年7月6日2023年1月15日食塩水の濃度実用数学技能検定（数学検定数検),数検3級

読了時間: 約4分36秒

Lukia

さぁ、早くも「食塩水に『水』を混ぜ合わせる問題」も最終回となってしまいました。
さっそく以下の問題を解いてみましょう。
解けたら、スクロールして、答え合わせをしてみてくださいね。

[mathjax]

問題

質量パーセント濃度が20%の食塩水に80gの水を加えたら、濃度が12%になった。
はじめの食塩水に溶けていた食塩の重さは何gか。

表に書き込む。

もも

表を描くのはいつもどおりですね。
横長の線を3本と、それを4等分できるように、
縦の線を3本引きます。

Lukia

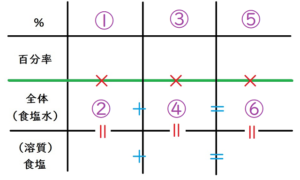
ももちゃんは、以下のような表を描いています。

もも

次に表の中に、数字や文字を書き込んでいきます。
まず、①は20、
②が80・・・

もも

いや、「80ｇの水を加えた」とあるから、
④が80　になるんだ！

Lukia

おっ、よく読めましたね。
ということは、③は、何ですか？

もも

③は、水が「0％食塩水」であることから、
0　が入ります。

もも

ということは、②をひとまず　$\Large x$ としておいてもいいですか？

Lukia

そうですね。
ということは、全体の重さの段は、「横はたし算」をしますから、
②+④=⑥となり、
⑥は、$\Large x+80$ となりますね。

もも

では、できあがりの食塩水の濃度が12％ということなので、
⑤が12となります。

％を百分率に直しておく。

Lukia

①から⑥がうまったので、まずは％を百分率に直してください。

もも

はい。
左から、
$\Large \frac{20}{100}$ ・ $\Large \frac{0}{100}$ ・ $\Large \frac{12}{100}$ です。

縦はかけ算・横はたし算

Lukia

では、それぞれの縦の列について、「縦はかけ算」をして、
表の一番下の段のマスをうめていきましょう。

もも

20％の食塩水の列は、
$\Large \frac{20}{100}\times x$ となります。

Lukia

ちなみに、今回求めるのは、何ですか？

もも

ええっと・・・
あっ、「はじめ20％の食塩水に溶けていた食塩の重さ」です。

Lukia

ということは、全体の重さ $\Large x$ を求めるだけではダメ。ということですね。
求める食塩の重さを $\Large y$ とおくと、
20％の食塩水の列は、別の表現ができますね。

もも

別の表現・・・
20％の食塩水の列の一番下のマスは、
$\Large \frac{20}{100}\times x$ でもあり、
$\Large y$ でもあるから・・・

もも

あっ！
$\Large y=\frac{20}{100}\times x$ だ！

Lukia

御明察です♪
これが後で効いてきますよ～。

もも

へ～。じゃ、次に進んで、
水、つまり、「0％食塩水」の列は、
$\Large \frac{0}{100}\times 80$ となるので、
一番下の段のマスには、$\Large 0$ を書き込みます。

もも

12％の食塩水の列は、
$\Large \frac{12}{100}\times \left( x+80\right)$ となります。

一番下の段の「たし算」をする。

Lukia

今回も順調ですね。
それでは、一番下の段の「横はたし算」をして、式を立ててください。

もも

はい。
式は、 $\Large \frac{20}{100}\times x+0=\frac{12}{100}\times \left( x+80\right)$
すなわち、
$\Large \frac{20}{100}\times x=\frac{12}{100}\times \left( x+80\right)$ となります。

Lukia

そうですね。それでは、計算については、ふきだしからはずして行うことにしましょう。

$$\Large \frac{20}{100}\times x=\frac{12}{100}\times \left( x+80\right) ・・・①$$
$$\Large y=\frac{20}{100}\times x ・・・②$$
式①の両辺の分母の100をはらって、
$$\Large 20x=12\left( x+80\right)$$
$$\Large \left( 20-12\right)x=12\times 80$$
両辺を8でわって、
$$\Large x=12\times 10$$
この値を式②に代入して、
$$\Large y=\frac{20}{100}\times 120$$
$$\Large y=24$$

こんなやり方もあります。

Lukia

せっかく、②の式も立てたのですから、先にこれを変形して、
①に代入することもできますね。
その計算方法も示してみます。

$$\Large \frac{20}{100}\times x=\frac{12}{100}\times \left( x+80\right) ・・・①$$
$$\Large y=\frac{20}{100}\times x ・・・②$$

Lukia

式②の両辺に逆数、すなわち、
$\Large \frac{100}{20}$ をかけます。

$$\Large \frac{100}{20}\times y=\frac{100}{20}\times \frac{20}{100}x$$
$$\Large x=5y$$
これを式①に代入します。
$$\Large \frac{20}{100}\times 5y=\frac{12}{100}\times \left( 5y+80\right) $$
両辺の分母の100をはらって、
$$\Large 20\times 5y=12\left( 5y+80\right)$$
$$\Large \left( 20-12\right)\times 5y=12\times 80$$
両辺を40でわって、
$$\Large y=24$$

もも

なるほど、①の式を計算しておいてから、②の式に代入してもいいし、
②の式を先に変形してから、①の式に代入してもいいんですね。

Lukia

そうです。
というわけで、こたえは、24ｇとなります。