数学検定準一級 第322回個別成績票を分析してみた。

2018年8月26日2023年1月15日数学検定準1級実用数学技能検定（数学検定 数検),数検準1級

2018年7月22日実施の第322回実用数学技能検定（以下数検）の個別成績票が送られてきました。
これによって、自分の解答の正確な正誤がわかったと同時に、
ぼんやりと自分、または他の受検者さんたちの現状もわかりました。

つたないですが、少し分析してみましたので、
第327回（10月28日）の対策の助けにしていただければ幸いです。

結論。「個別成績票」はさらっと見て、さっさと勉強しよう。

「個別成績票」とはいいますが、ざっくり感は否めないです。
私の場合、1次の計算技能検定は、〇か×かがついているだけでした。
1次に部分点があったのかどうかはわかりません。

2次の数理技能検定は、1問につき1点で、
部分点は、0.2など小数点でついていました。
（10倍したほうがわかりよいと思うのですが・・・）

受検日から1か月以上経っていますし、
2次に関しては、解答を書き写す余裕もなかったので、
どんな解き方をして、この点数だったのか。というのを正確に再現することは難しいです。

というわけで、ざっくりと、どこの単元を勉強しなおすべきか。ぐらいしかわかりません。

これまた文句ばっかり言ってて、申し訳ないのですが、
「どこの単元を勉強しなおすべきか。」を把握することも、個別成績票だけでは完結しないのです。

たとえば、模擬試験ですと、成績票には、どこの単元のなんという事項が出題されているのか。みたいなのが書いてありますし、もちろん点数もわかるので、
成績票を見るだけで、「ああ、私はここの単元（事項）を勉強しておかないといけないんだな。」などとわかるのですが、
数検の成績票は、問題冊子、または個別成績票と一緒に送られてくる模範解答を見て、なんとなく出題範囲を推測するしかありません。

というわけで、心待ち（？）にした個別成績票ですが、
得点の根拠となる正誤だけがわかるだけのざっくりしたものでしたので、
「なるほどねぇ。第322回は〇点だったのね。」というぐらいにして、

さっさと勉強に取り掛かるほうがよいと思いました。

「受検者全体に関する情報」を読み解く。

とはいえ、全受検者と比較して自分はどうか。ということが読み取れそうなグラフがあれこれ載っておりましたので、
少し読み解いてみようかと思います。

「受検者全体に関する情報」として、ヒストグラム（棒グラフ）がありました。
これを箱ひげ図（数学Ⅰで習います。）に変換してみました。
ただし、パソコンで箱ひげ図を描くのが難しかったので、
帯状のグラフにしています。

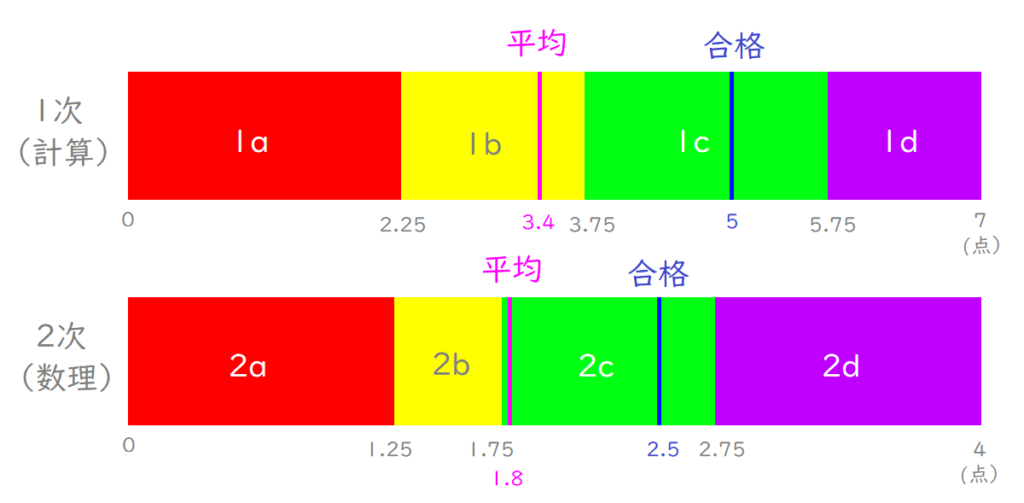
ヒストグラムをなるべく正確に読み取って、全受検者を4等分しました。
つまり、25％ずつの人が、赤・黄・緑・紫の帯に振り分けられています。
また、帯の下にある灰色の数値は、これまただいたいの点数（値）です。

まぁ、とにかく、ざっくり全体の状況と、自分の位置を把握してみましょう。

（大学）受験生は、まず合格してから「受検」しましょう。

まず、1次の合格率は、34.8%、2次の合格率は31.9％でした。
まぁまぁ難しい部類の検定だといえますね。

ということは、生半可な気持ちでチャレンジしちゃダメってことです。

以前別の記事でも書きましたが、大学入試の前哨戦みたいなつもりで受けるのはやめたほうがいいと思います。

志望校の過去問と、数検ホームページにあるサンプル問題を比較してみてください。
傾向が全く同じですか？
そうでないなら、受験料4500円は別の模擬試験や、参考書代に使いましょう。

また、7月8月の時点で、大学受験に関して完全無欠の状態ですか？
「もうやることがな～い。」という人以外は、
やっぱり、無事大学に合格して、まだ数学のカンが鈍っていない春ごろに受検されるほうがよいと思います。

1次（計算技能検定）について。

さて、グラフから読み取ったことを箇条書きにしてみます。

1. 平均点が5割を切っている。
2. 平均点が中央値を下回っている。

本当はまだまだ読み取れるんでしょうが、私の力ではこのぐらいです。

1.　平均点が5割を切っている。

ほとんどの試験は、平均点が6割になることを目指して作られています。
（実際にはそうはならないのですが）
おそらく、数検も平均点が6割になるような作問を心がけていると思います。

ちなみに、平均点が6割というと、4.2点ですから、今回の帯グラフでは、緑色の1cのエリアに位置します。
ところが、平均点は、黄色の1bエリアに位置していますね。

また、「合格点と平均点の間の幅」に注目してみます。
合格点は、数検側が設定しているので、固定されています。
一方、平均点は、受検者の得点状況によって変動します。
ということは、この幅が狭ければ、「受検者全体がよく勉強できている。」ということを示し、
幅が広ければ、「勉強不足の受検者が多いか、試験として破綻している（難しすぎる）。」ということを示しています。

ここで、1次と2次の「合格点と平均点の間の幅」を比較してみると、
1次の幅は、2次の幅の2倍以上の開きがあります。

2.平均点が中央値を下回っている。

中央値というのは、全体の受検者のちょうど真ん中の順位の人が取る値のことです。
帯グラフでは、赤と黄色で全受検者の下位50％を占め、
緑と紫が上位50％を構成していることになります。
受検者の2人に1人が、3問正答するのがせいいっぱい。という状況ということになりますね。

計算技能検定の平均点が低めな理由を考えてみる。

印象としては、計算技能検定の問題は、決して難しいものではありません。
高校数学の問題集などで練習すれば、十分対応できる内容だと思います。
しかし、それなのに、2次の平均点よりも下回っているのはなぜなのか。

まず、第一に考えられるのは、受検者全体が、計算問題の知識不足・練習不足ということです。

そしてもうひとつは、採点形式の違いにあるかと思います。

計算問題では、部分点を期待しにくい。

1次の計算技能検定では、ほとんどが〇か×しかなく、部分点が見込めないのだろうと思います。
部分点があるとすれば、第322回ですと、問1（解が2つあった）と問5（①で不定積分、②で定積分を求める）ぐらいでしょうか。
もしかしたら、問3の値が4桁でしたので、1の位が少し違うぐらいなら、（計算ミス）部分点がもらえたかもしれません。
（ま、ないと思いますが）

数学準一級範囲は、計算力あってこそ。

数検準1級の主な範囲は、高校数学でいうと、数学Ⅲにあたります。
数学Ⅲは難しいことをやっているように思いますが、ほとんどが「ちょっと難しい計算問題」です。

「ちょっと難しい」と書きましたが、そう思えるようになるには、「慣れるための練習」が必要です。

『カルキュール』など計算問題に特化した問題集を使って、たっぷり練習することをオススメします。

カルキュール数学3改訂版 基礎力・計算力アップ問題集 （駿台受験シリーズ） [ 上田惇巳 ] 価格：918円（税込、送料無料) (2019/4/19時点) 楽天で購入

帯の色ごとに対策を考えてみる。

帯グラフの理想は、平均点と合格点との幅が狭くなり、黄色、または赤の帯が合格ラインに近づくことです。
それぞれの帯について、現状や対策を考えてみたいと思います。

赤（1a）の人。

明らかに「知識不足」です。
2問正答するのがやっと。という状況だといえます。
また、一部高校数学ですと、ⅡB範囲の問題が3問含まれていました。

数学Ⅲ範囲は、ⅠA・ⅡB範囲のしっかりした基礎があってこそ解けるものなので、
まずは、ⅡB範囲（数検2級レベル）の問題集を解いて、基礎をしっかりさせることが必要だと思います。
数検2級の計算・数理の問題を解きまくり、弱点をなくしましょう。

赤エリアを脱出する人が多くなれば、全体的な底上げになります。

黄色（1b）の人。

このエリアの人たちは、「練習不足」です。
ⅡB範囲の問題が怪しい人も含まれているようですので、
『カルキュール』や、『過去問題集』、『発見』などの「計算技能検定」分野を集中的に練習しましょう。
同じ問題を何周も解くのは、一見無駄なように思えますが、手順を体に覚えこませる、スピードアップを図るには練習あってこそですので、どんどんやりましょう。
何周かするうちに、問題がふるいにかけられ、どうしても苦手な問題がわかってきます。検定直前は、それだけを見直せばよいので、効率的な勉強ができるようになりますね。

緑（1c）の人。

このエリアには、「経験不足」の人が含まれています。
合格圏内であり、あとひといき。ということになりますね。
対策は、黄色エリアと同様ですが、問題に対する知識や、計算のスピードはそこそこ問題のない状態にあると思いますので、
検定範囲の問題をあれこれやって、苦手な問題、難しい問題をあぶりだし、重点的に練習していきます。

紫（1d)の人。

「計算技能」はひとまず、問題なしといえます。
しかし、今回問題5の積分の正答率が低い状態でした。
これは、全体だけでなく、合格者もここだけ低かったです。

三角関数がらみの積分は、どうやら数検が大好きなパターンのようなので、
あれこれと自分でバリエーションを作ってやってみることをオススメします。

2次（数理技能検定）の分析。

1次のほうにかなり力を入れたので、息切れしてしまいました。
ボリュームが少なくて物足りないかもしれませんがご容赦ください。

意外とイイ感じの帯グラフになっている理由。

1次と2次の帯グラフを比べてみると、中央値（黄色の右端）の位置や、平均点と合格点との幅に差があることがわかります。
2次は、緑（2ｃ）と紫（2d)の幅が広く、合格圏内、または合格射程圏内の割合が多くなっています。

この理由について私が考えたのは以下の二つです。

1. 1次合格者が含まれている。
2. 部分点がある。

1.1次合格者が含まれている。

2次の受検者には、「ひとまず計算力には問題がない1次合格者」が含まれているので、底上げはされているといえます。
赤エリア、黄色エリアの人は、数理技能検定の出題形式に慣れていないことが考えられますので、
合格するには、相変わらず計算力を落とさないように心がけ、過去問にたくさん触れながら経験を増やすことが重要だと思います。

2.部分点がある。

1次は、基本、〇か×かしかないので、ある意味リスクが高いのですが、
2次は、部分点が設定されているので、完答できなくても総合的に点数が稼げる可能性があります。
選択問題のジャンルをしぼって、集中的に勉強・練習し、完答を目指すのもアリだと思います。

2次問題選択状況

受検者全体・合格者ともに「行列」の問題を選択している人が少なめでした。
あとで、「受検者および合格者の年齢構成」にも触れますが、

現在、高校数学において、「行列」は範囲外となっておりますので、
受検者の半分を占める10代は、学校で習ってないので選びにくい状況にあります。

また、範囲外なので、高校数学レベルで、「行列」を勉強できる本が出回っていないのも、
「行列」選択者の数を下げる理由となっていると思います。

受検者および合格者の年齢構成について。

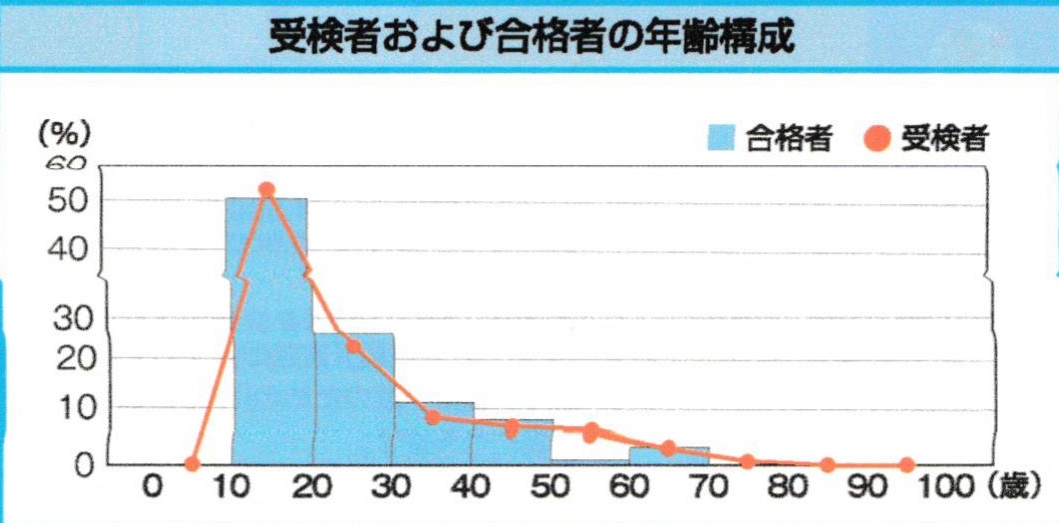
10代の受検者が最も多く、全体の半分を占めています。
私が受検した会場でも、18～20歳ぐらいの若い男性が多かったので、
理系男子が多く受検するんでしょうね。

高校3年生～大学生が多く受検し、30代以降は、受検者数がゆるやかに減少していきます。
オレンジ色の折れ線グラフを見る限りでは、どうやら70代の方も挑戦されているようです。

いつまでも、学び続けようという姿勢はすばらしいなぁ。と思いました。
私も、まだまだがんばらねば。

合格者については、50代の合格率が著しく低いのも驚きました。

これは、私の推測なのですが、
年齢的に、職場では重責のある管理職だったり、
家庭では、高校生や、大学生ぐらいのお子さんがいるなどして、
自分の勉強よりは、ほかにやらねばならないことに忙殺されて、
効率の良い勉強ができていないのかもしれませんね。

60代は、受検者数と合格者数がほぼ一致しているので、
退職されたり、お子さんが巣立って、余裕のある環境となり、
しっかり勉強された結果が表れているのだろうと思います。

現役または元受験生の10代も、60代と同様、
受検者数と合格者数がほぼ一致しているので、
数学によくふれあい、しっかり対策を立てていれば確実に合格できる検定なのだといえますね。

記事を書きながら、希望が湧いてきました。

Leave This Blank:Leave This Blank Too:Do Not Change This:

メールアドレス：