2019年大学入試センター試験数学1A「第5問図形の性質」を解いてみる。

2019年1月26日2023年1月14日図形の性質,大学入試センター試験実用数学技能検定（数学検定数検),数検2級,数検準2級

読了時間: 約5分57秒

[mathjax]

問題

$ \ \triangle \mathrm{ABC} \ $において,$ \ \mathrm{AB}=4 \ , \ \mathrm{BC}=7 \ , \ \mathrm{AC}=5 \ $とする。
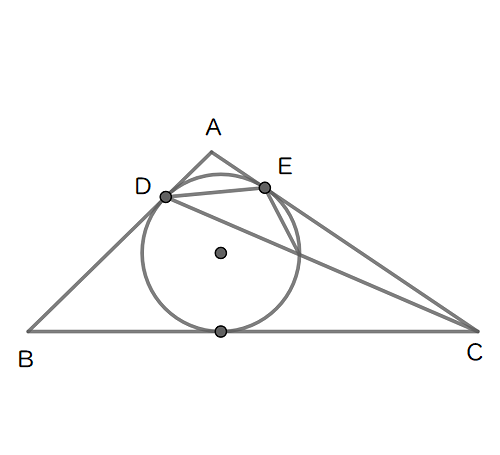
このとき,$ \ \cos \angle \mathrm{BAC}=-\frac{1}{5} \ ,\quad \sin \angle \mathrm{BAC}=\frac{2\sqrt{6}}{5} \ $　である。
$ \ \triangle \mathrm{ABC} \ $の内接円の半径は$ \ \color{#0004fc}{\frac{\sqrt{ア}}{イ}} \ $である。
この内接円と辺$ \ \mathrm{AB} \ $との接点を$ \ \mathrm{D} \ $,辺$ \ \mathrm{AC} \ $との接点を$ \ \mathrm{E} \ $とする。
$ \ \mathrm{AD}=\color{#0004fc}{ウ} \ , \ \mathrm{DE}=\color{#0004fc}{\frac{エ\sqrt{オカ}}{キ}} \ $　である。

$$\begin{align}\triangle \mathrm{ABC}の面積を \ &\mathrm{S} \ とする. \\\\ また内接円の半径を \ &r \ とする. \\\\ \mathrm{S}=&\frac{1}{2}\cdot 4\cdot 5\sin \angle \mathrm{BAC}=\frac{1}{2}\left( \mathrm{AB}+\mathrm{BC}+\mathrm{CA}\right)r\\\\ 8\sqrt{6}=&16\mathrm{I}\\\\ r=&\color{#0004fc}{\frac{\sqrt{6}}{2}} \end{align}$$
$$\begin{align}\mathrm{AD}=&a \ , \ \mathrm{DB}=b \ , \ \mathrm{CE}=c\quad とする。 \\\\ \mathrm{AB+BC+CA}=&2\left( a+b+c\right) \\\\ a+b+c=&8\\\\ b+c=&7\quad より\\\\ a=&1\\\\ \mathrm{AD}=&\color{#0004fc}{1} \end{align}$$
$$\begin{align}\triangle \mathrm{ADE} \ において&余弦定理より \\\\ \cos \angle \mathrm{DAE}=&\frac{1+1-\mathrm{DE}^2}{2\cdot 1\cdot 1} \\\\ \mathrm{DE}=&\color{#0004fc}{\frac{2\sqrt{15}}{5}} \end{align}$$

問題

線分$ \ \mathrm{BE} \ $と線分$ \ \mathrm{CD} \ $の交点を$ \ \mathrm{P} \ $,
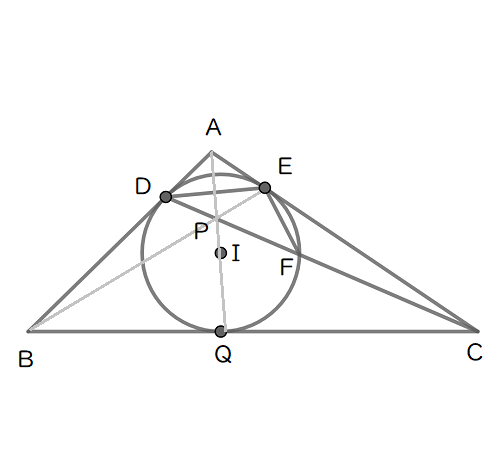
直線$ \ \mathrm{AP} \ $と辺$ \ \mathrm{BC} \ $との交点を$ \ \mathrm{Q} \ $とする。
$ \ \mathrm{\frac{BQ}{CQ}}=\color{#0004fc}{\frac{ク}{ケ}} \ $　であるから,　$ \ \mathrm{BQ}=\color{#0004fc}{コ} \ $　であり,
$ \ \triangle \mathrm{ABC} \ $の内心を$ \ \mathrm{I} \ $とすると
$ \ \mathrm{IQ}=\color{#0004fc}{\frac{\sqrt{サ}}{シ}} \ $　である。
また,直線$ \ \mathrm{CP} \ $と$ \ \triangle \mathrm{ABC} \ $の内接円との交点で$ \ \mathrm{D} \ $とは異なる点を$ \ \mathrm{F} \ $とすると
$ \ \cos \angle \mathrm{DFE}=\color{#0004fc}{\frac{\sqrt{スセ}}{ソ}} \ $　である。

$$\begin{align}\mathrm{\frac{BQ}{CQ}}=&\color{#0004fc}{\frac{3}{4}}\quad より \\\\ \mathrm{BQ}=&\color{#0004fc}{3} \\\\ 点 \ \mathrm{Q} \ は& \ 内接円 \ \mathrm{I} \ 上の点であるから\\\\ \mathrm{IQ}=&\color{#0004fc}{\frac{\sqrt{6}}{2}}\end{align}$$

Lukia

三角形の内心は、それぞれの角の二等分線の交点です。
また、内心から辺におろした垂線の長さを半径とする内接円が描けます。

$$\begin{align}\triangle \mathrm{ADC}において, \quad &余弦定理より \\\\ \mathrm{DC}=&2\sqrt{7} \\\\ \triangle \mathrm{CDE} \ と \ \triangle \mathrm{CEF} \ において&接弦定理より\quad \\\\ \angle \mathrm{CDE}=\angle \mathrm{CDE} \ \cdots\cdots \ ①\\\\ &\angle \mathrm{ECD}=\angle \mathrm{FCE} \ \cdots\cdots \ ②\quad より\\\\ &\triangle \mathrm{CDE} \sim \triangle \mathrm{CEF}\end{align}$$
$$\begin{align}ここで, \\\\ \cos \angle \mathrm{DFE}=&-\cos \angle \mathrm{EFC}=-\cos \angle \mathrm{DEC} \\\\ 余弦定理より& \\\\ -\cos \angle \mathrm{DEC}=&\frac{\frac{60}{25}+16-28}{2 \cdot \frac{2\sqrt{15}}{5}\cdot 4}\\\\ =&\frac{48}{16\sqrt{15}}=\frac{\sqrt{15}}{5}\\\\ ゆえに\quad \cos \angle \mathrm{DFE}=&\color{#0004fc}{\frac{\sqrt{15}}{5}} \end{align}$$

Lukia

接弦定理・相似比などをバンバン使う問題なので、私は第5問はあまり選びませんでした。幾何は、図形のイメージ力とか、くるくると視点を変えられるかどうかなどが求められる、数学の中でも瞬発力重視の分野だと思います。
私の場合、加齢によりここらへんの感覚や瞬発力が鈍っていたので、特に苦手意識がありました。

Lukia

最後の$ \ \cos \angle \mathrm{DFE} \ $を求めるためには、その外角を含む$ \ \triangle \mathrm{CEF} \ $を用いたくなると思いますが、そうなると、辺$ \ \mathrm{EF} \ $を求める必要が出てきます。
すると、相似比から求める手間が増えますね。
相似とは、拡大・縮小の関係ですから、すでに三辺の辺の長さがわかっている$ \ \triangle \mathrm{CDE} \ $を用いても、なんの不都合もありません。

Lukia

このように、シンプルなことに気が付けば、手間が省けるようになっているのが、センター数学だといえるでしょう。
必要以上に焦ったり、緊張したりすると、パフォーマンス度はどんどん下がってしまいます。
「焦るな！」とか、「緊張するな！」と思えば思うほど、ドツボにはまってしまうので、
「ああ、ちょっと焦ってるな。」とか、「あれ、ちょっと緊張しすぎ？」と事実を受け入れるようにしましょう。
交感神経があまりに優位になりすぎても、パフォーマンスはよくなりません。
やったこと以上の成果なんて出ませんから、むしろ落ち着いて、やったことを100パーセントに近い状態で発揮できるようにしましょう。

Lukia

そういえば、わたくしごとなのですが、
今回の図は、GeoGebra（ジオジブラと読むのかな？）のスマホアプリ版で描きました。
GeoGebra自体は、パソコン版をインストールして数ヶ月経っているのですが、
これまで、使い方がよくわからない、試行錯誤する時間的余裕がない。などの理由で、ずっと使えずにいました。
式が立てられるグラフは、GRAPESで描くことができたのですが、（これも、なんとなく試行錯誤しているうちにできるようになった）
GeoGebraはさっぱりわからず・・・。
結果、ペイントなどで、それらしい図形を描いてごまかしてきました。
今後は、図形もきれいなものが描けそうなので、うれしいです。

2019年大学入試センター試験の数学の問題の一覧です。