人柄は解法に表れる

2022年6月19日2023年1月8日数と式大学入学共通テスト,実用数学技能検定（数学検定 数検),数検2級,数検3級

インスタグラムで#mathmaticsをフォローしています。
タイムラインでちょっとおもしろい？問題が流れていましたので、解いてみます。

解法

2つの式より、\( \ x,y \ \)はともに\( \ 0 \ \)以上の整数と考えられる。
また、①より\( \ x \ \)は整数の2乗と考えられるので、 \( \ x=0, \ 1, \ 4, \ 9, \ 16, \ \cdots n^2 \ \)(\( \ n \ \)は自然数）
さらに②より、\( \ y \ \)も整数の2乗である必要がある。
②を変形して、
$$\begin{align}\sqrt{y}=11-x &\gt 0 \\\\ 11& \gt x\quad \rm{より} \end{align}$$ \( \ x=0, \ 1, \ 4, \ 9 \ \) のいずれかである。
求めた\( \ x \ \)をそれぞれ①に代入する。
ⅰ）\( \ x=0 \ \) のとき \( \ y=7 \ \)
ⅱ）\( \ x=1 \ \) のとき \( \ y=6 \ \)
ⅲ）\( \ x=4 \ \) のとき \( \ y=5 \ \)
ⅳ）\( \ x=9 \ \) のとき \( \ y=4 \ \)

ここで、ⅰ）〜ⅳ）のうち、\( \ y \ \)の値が整数の2乗を満たすのはⅳ）だけである。
ゆえに、\( \ x=9, \ y=4 \ \)

こたえ

\( \ x=9, \ y=4 \ \)

数学に「暗黙の了解」はないと思え。

インスタの出題者さんは、ベルギーの方のようで、解法動画へ誘導されていました。
なかなか複雑な解き方をしていらっしゃいまして、最後の方は魂抜けてましたね。(笑)

ちなみに、今回の問題に「\( \ x \ \)や\( \ y \ \)が整数である」という条件をつけたのは私です。

というのも、グラフ描画アプリで試してみると、解が2つ出てきちゃったからなんです。

与えられた式を
\( \ \begin{eqnarray} \left\{ \begin{array}{l} y = 7-\sqrt{x} \\ y = \left( x-11\right)^2 \end{array} \right. \end{eqnarray} \ \)
と変形します。
これをグラフ描画アプリに入力したものが、以下のグラフです。
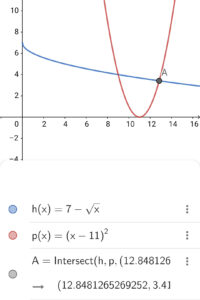2つの曲線は2点で交わっていることがわかります。
特になんの文字も充てていない交点が、今回求めた整数解です。
\( \ x=11 \ \) を超えても解があることに驚き、上の解法でなぜ答えが見つからないのかを調べてみました。
この交点を\( \ \mathrm{A} \ \)とし、その値を見てみると、無理数のようでした。

インスタの出題者さんは、数について何の限定もしていなかったのですが、
もしこれが、「ただし、\( \ x, \ y \ \) は実数とする」なんてやられたら、交点\( \ \mathrm{A} \ \)も求めないといけなくなったことでしょう。（これなら、ラマヌジャンじゃないと無理かも）


もし、これが大学入試などだったら、（数についての条件がないと仮定）
「私が解けるのはこの範囲内です！」と宣言して解くことで、分をわきまえた、真摯な人柄が伝わるかもしれません。（少なくとも私はそう思う）

何も断らずに、整数解だけをぽんと書くと、
試験官：「あれ？これ、グラフを描けば実数解は2つあることがわかるよね。なんで、一個だけ答えてるの？」
受験生：「だ〜って、整数解だと思うじゃ〜ん。」
試験官：「自分には整数解しか無理って断らないと。試験官はあなたより頭がいいんだから、あなたの実力がどの程度かなんて言わなくてもわかってくれると思った？そういうとこ真摯じゃないよね。」
受験生：「・・・。」

数学なのに、漢字や日本語を結構書かなければいけないのは、自分が遊んだ範囲（条件）を限定し、提示するためなんです。
これをめんどくさがって省略すると、口頭試問でもあったら徹底的にやりこめられると思います。(笑)
（少なくとも私ならそうする）

どんな間柄でも、安易な同一視は無礼・失礼にあたります。
それは学問の世界でも同じ。

「なんて言ったらいいんだろう、わきゃ〜」となりながらでも、自分の考えをアウトプットする練習を繰り返してください。

試験官の見たいのは、そういう悪戦苦闘する姿なのです。

Leave This Blank:Leave This Blank Too:Do Not Change This:

メールアドレス：